1. 概述
这是字典树之旅系列文章的第三篇,第一篇介绍了 Trie 的基本概念,第二篇介绍了 Trie 的标准实现。
阅读前文,我们可以发现标准实现有一个非常大的缺点:每个字符一个节点,每个节点有一个容量为 R 的数组,因此在稀疏数据集中会有严重的空间浪费。
那么,这一篇文章我们就来介绍一下其变体: Patricia Trie [^3]。
注 1:Patricia Trie 或是 Patricia Tree, 在一些论文中又称其为 compact trie(紧凑 trie),或 compressed trie(压缩 trie)。
注 2:Patricia 的全称是”检索字母数字编码信息的实用算法“(practical algorithm to retrieve information coded in alphanumeric),是 Morrison 于 1968 年提出的数据结构,原论文是二进制位比较的形式,有兴趣的话可以阅读参考资料 3。
2. 基本介绍
Patricia Trie 是 Trie 的一种简单变体,如果一个非根节点仅有一个子节点,则将其子节点与该节点合并。
文字描述稍有点抽象,还是看图:
节点合并

图1:节点合并
节点分裂
如果需要添加键 "bc",该如何来处理哪?我们需要将 "bcd" 分裂成两个节点,效果见下图:
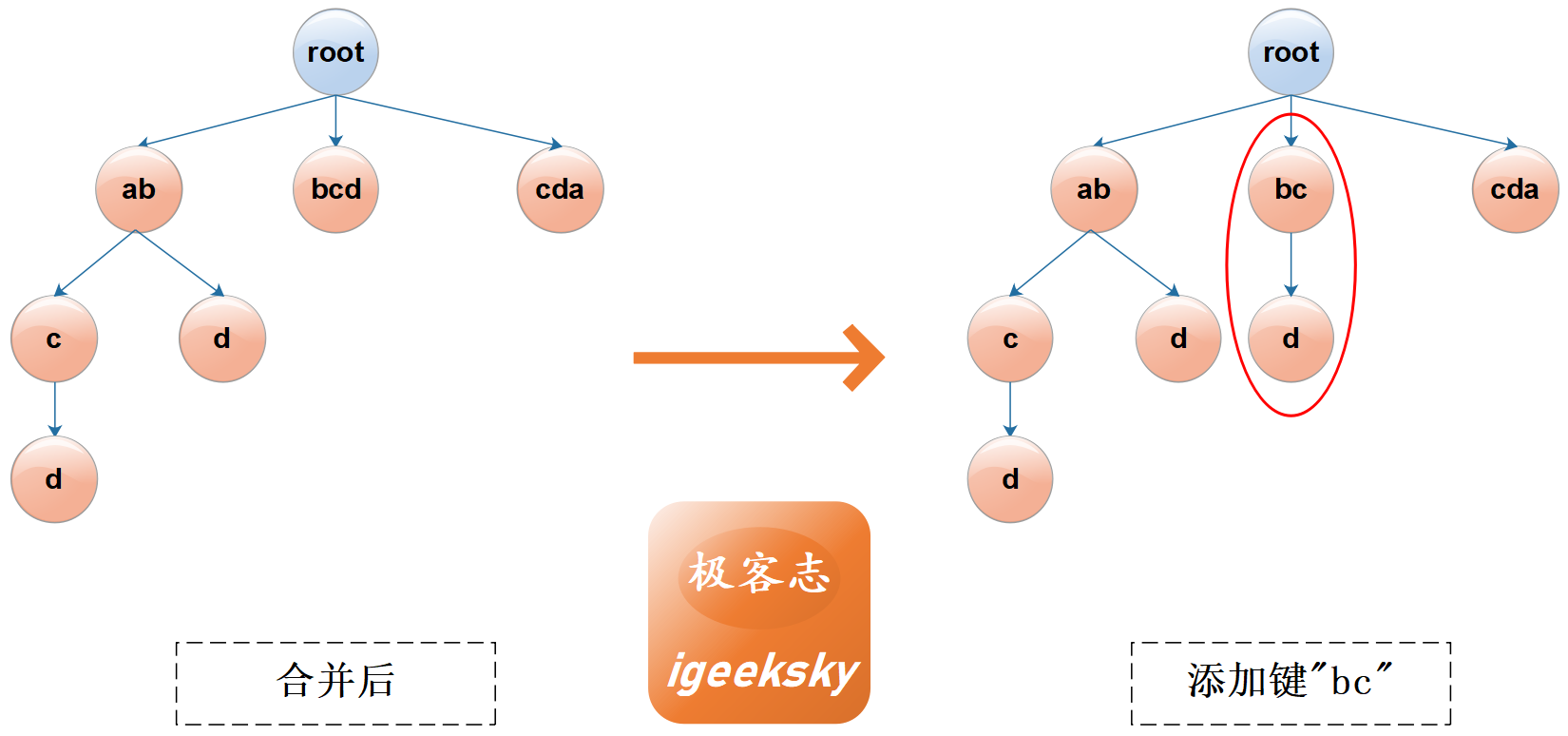
图2:节点分裂
相信,这两张图已足以说明一切😀
同时,我们也可以看到合并后节点数变少,因此减少了可能的内存消耗。
3. 树的实现
依照惯例,还是写代码来实现它。
3.1. 节点定义
package com.igeeksky.perfect.nlp.trie;
private static class PatriciaNode<V> {
// key的一部分 String subKey;
// 值(支持泛型,可以是非字符串) V val;
// 子节点 PatriciaNode<V>[] table;
public PatriciaNode(int R) { this.table = new PatriciaNode[R]; }
public PatriciaNode(int R, String subKey) { this.subKey = subKey; this.table = new PatriciaNode[R]; }
public PatriciaNode(String subKey, V value) { this.subKey = subKey; this.val = value; }
public PatriciaNode(int R, String subKey, V value) { this.subKey = subKey; this.val = value; this.table = new PatriciaNode[R]; }}
复制代码
对比前文的 StandardNode,我们可以看到多了一个 String 类型的 subKey 字段,该字段用于存储节点合并之后的字符串,其它没有变化。
3.2. 方法实现
这里继续沿用前文介绍的 Trie<V> 接口(接口介绍见上一篇文章)。
3.2.1. put 方法
public class PatriciaTrie<V> implements Trie<V> {
private int size; private static final int R = 65536; private final PatriciaNode<V> root = new PatriciaNode<>(R);
/** * 添加键值对 * * @param key 键 * @param value 值 */ @Override public void put(String key, V value) { int last = key.length() - 1; if (last < 0) { return; } PatriciaNode<V> node = root; for (int i = 0; i <= last; i++) { char c = key.charAt(i); // 判断数组是否为空,如果为空则创建数组 if (node.table == null) { node.table = new PatriciaNode[R]; } // 通过字符查找子节点,如果子节点不存在则创建子节点并返回,否则与子节点进行字符串比较 PatriciaNode<V> child = node.table[c]; if (child == null) { node.table[c] = new PatriciaNode<>(key.substring(i), value); ++size; return; } String subKey = child.subKey; int subLast = subKey.length() - 1; // 与子节点进行字符串比较 for (int j = 0; j <= subLast; j++, i++) { // 字符相同 if (subKey.charAt(j) == key.charAt(i)) { if (i == last) { if (j == subLast) { // 直到最后一个字符都完全相同,无需分裂 if (child.val == null) { ++size; } child.val = value; } else { // 新增键较短,子节点分裂成两个节点,无新的分支节点,例:原有 bcd,新增键bc ——> bc, d PatriciaNode<V> child0 = new PatriciaNode<>(R, subKey.substring(0, j + 1), value); node.table[c] = child0; child.subKey = subKey.substring(j + 1); child0.table[child.subKey.charAt(0)] = child; ++size; } return; } if (j == subLast) { break; } } else { // 字符不同 // 子节点分裂成两个节点,再加上新的分支节点,例:原有 bcd,新增键 bca ——> bc, d, 新分支a PatriciaNode<V> child0 = new PatriciaNode<>(R, subKey.substring(0, j)); node.table[c] = child0;
child.subKey = subKey.substring(j); child0.table[child.subKey.charAt(0)] = child; // 新分支 PatriciaNode<V> child1 = new PatriciaNode<>(key.substring(i), value); child0.table[child1.subKey.charAt(0)] = child1; ++size; return; } } node = child; } }}
复制代码
对比 StandardTrie,代码稍微复杂了一些,多了与子节点进行字符比较的逻辑。另外,从代码也可以看出,其时间复杂度依然是 O(m),m 为字符串长度。简单画了张图来描述这部分新增逻辑:
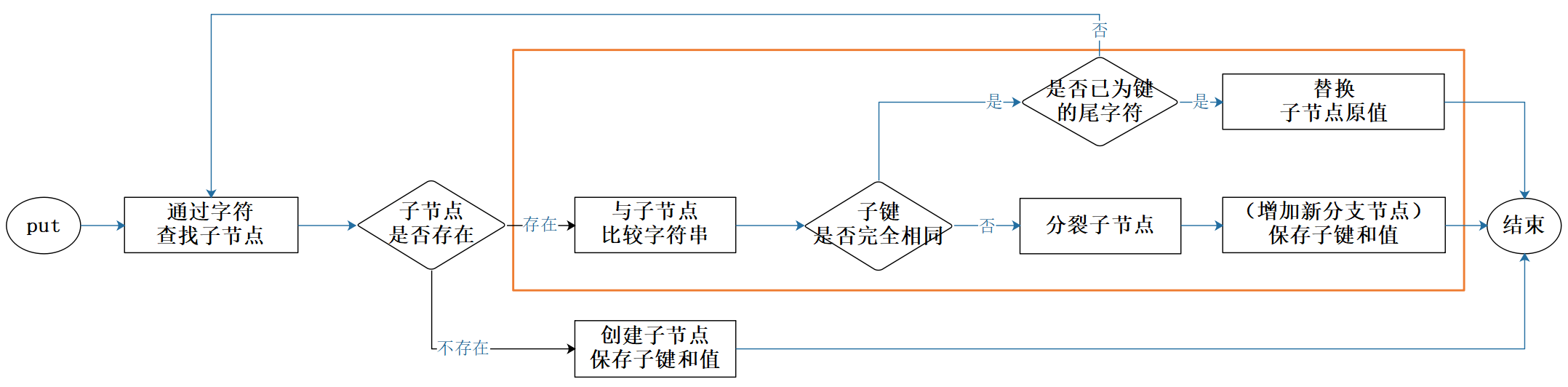
图3:PatriciaTrie put方法
注:与子节点进行字符串比较的逻辑其实可以放到 PatriciaNode 中,这样代码会更加清晰可读。因需与前文比对新增逻辑,所以还是放在了这里。
3.2.2. get 和 remove
public class PatriciaTrie<V> implements Trie<V> { /** * 获取键关联的值 * * @param key 键 * @return 值 */ @Override public V get(String key) { PatriciaNode<V> node = find(key); return (node == null) ? null : node.val; }
/** * 通过键查找节点 * * @param key 键 * @return 键的对应节点 */ private PatriciaNode<V> find(String key) { int last = key.length() - 1; if (last < 0) { return null; } PatriciaNode<V> node = root; for (int i = 0; i <= last; i++) { if (node.table == null || (node = node.table[key.charAt(i)]) == null) { return null; } String subKey = node.subKey; int subLast = subKey.length() - 1; for (int j = 0; j <= subLast; j++, i++) { if (subKey.charAt(j) == key.charAt(i)) { if (i == last) { if (j == subLast) { return node; } return null; } if (j == subLast) { break; } continue; } return null; } } return node; }
/** * 删除键值对(惰性删除) * * @param key 键 * @return 旧值 */ @Override public V remove(String key) { PatriciaNode<V> node = find(key); if (node == null) { return null; } V oldVal = node.val; if (oldVal != null) { // 惰性删除:仅把关联的值置空,没有真正删除节点 node.val = null; --size; } return oldVal; }}
复制代码
3.2.3. 查找给定字符串的最长前缀
/** * 前缀匹配:查找 word 的最长前缀 * * @param word 待匹配词(不为空且长度大于0) * @return 键值对 */ @Override public Tuple2<String, V> prefixMatch(String word) { int last = word.length() - 1; if (last < 0) { return null; } PatriciaNode<V> node = root; Tuple2<String, V> tuple2 = null; for (int i = 0; i <= last; i++) { if (node.table == null || (node = node.table[word.charAt(i)]) == null) { return tuple2; } String subKey = node.subKey; int subLast = subKey.length() - 1; for (int j = 0; j <= subLast; j++, i++) { if (subKey.charAt(j) == word.charAt(i)) { if (j == subLast) { if (node.val != null) { tuple2 = Tuples.of(word.substring(0, i + 1), node.val); } break; } if (i == last) { return tuple2; } continue; } return tuple2; } } return tuple2; }
复制代码
3.2.4. 查找以给定字符串为前缀的所有键
/** * 查找并返回以 prefix 开头的所有键(及关联的值) * * @param prefix 前缀(不为空且长度大于0) * @return 所有以 prefix 开头的键值对 */ @Override public List<Tuple2<String, V>> keysWithPrefix(String prefix) { List<Tuple2<String, V>> results = new LinkedList<>(); PatriciaNode<V> parent = find(prefix); if (parent == null) { return results; } traversal(parent, prefix, results); return results; }
/** * 深度优先遍历,将所有以 prefix 开头的键值对添加到结果集 * * @param parent 父节点 * @param prefix 前缀 * @param results 结果集 */ private void traversal(PatriciaNode<V> parent, String prefix, List<Tuple2<String, V>> results) { if (parent.val != null) { results.add(Tuples.of(prefix, parent.val)); } if (parent.table != null) { for (int c = 0; c < R; c++) { // 由于数组中可能存在大量空链接,因此遍历时可能会有很多无意义操作 PatriciaNode<V> node = parent.table[c]; if (node != null) { String key = prefix + node.subKey; traversal(node, key, results); } } } }
复制代码
3.2.5. 查找给定文本中包含的键
/** * 查找给定文本段中包含的键 * * @param text 文本段(不为空且长度大于0) * @return 结果集(键、值、键在文本中的起止位置) */ @Override public List<Found<V>> matchAll(String text) { List<Found<V>> results = new LinkedList<>(); int last = text.length() - 1; for (int i = 0; i <= last; i++) { matchAll(results, text, i, last); } return results; }
/** * 找到前缀节点后,遍历所有后缀节点,并将所有后缀节点包含的键值对添加到结果集 * * @param results 结果集 * @param text 文本段 * @param start 文本段的开始位置 * @param last 文本段的结束位置(末尾) */ private void matchAll(List<Found<V>> results, String text, int start, int last) { PatriciaNode<V> node = root; for (int i = start; i <= last; i++) { if (node.table == null || (node = node.table[text.charAt(i)]) == null) { return; } String subKey = node.subKey; int subLast = subKey.length() - 1; for (int j = 0; j <= subLast; j++, i++) { if (subKey.charAt(j) == text.charAt(i)) { if (j == subLast) { if (node.val != null) { results.add(new Found<>(start, i, text.substring(start, i + 1), node.val)); } break; } if (i == last) { return; } continue; } return; } } }
复制代码
以上就是 PatriciaTrie 的全部代码,代码逻辑还是比较简单的。
3.2.6. 单元测试
测试用例还是用之前的,换成 PatriciaTrie 继续测。
public class PatriciaTrieTest {
/** * 查找输入字符串的最长前缀 */ @Test public void prefixMatch() { PatriciaTrie<String> trie = new PatriciaTrie<>(); trie.put("abc", "abc"); trie.put("abd", "abd"); Tuple2<String, String> tuple2 = trie.prefixMatch("abcd"); Assert.assertEquals("abc", tuple2.getT2()); tuple2 = trie.prefixMatch("bcd"); Assert.assertNull(tuple2); }
/** * 查找所有以给定字符串为前缀的key */ @Test public void keysWithPrefix() { PatriciaTrie<String> trie = new PatriciaTrie<>(); trie.put("ab", "ab"); trie.put("abc", "abc"); trie.put("abcd", "abcd"); trie.put("abd", "abd"); trie.put("bcd", "bcd"); trie.put("cda", "cda"); List<Tuple2<String, String>> keysWithPrefix = trie.keysWithPrefix("ab"); Assert.assertEquals("[[ab, ab], [abc, abc], [abcd, abcd], [abd, abd]]", keysWithPrefix.toString()); keysWithPrefix = trie.keysWithPrefix("abcde"); Assert.assertEquals("[]", keysWithPrefix.toString()); }
/** * 查找给定文本段中包含的键 */ @Test public void matchAll() { PatriciaTrie<String> trie = new PatriciaTrie<>(); trie.put("abcd", "abcd"); trie.put("bcdef", "bcdef"); trie.put("abe", "abe"); List<Found<String>> matchAll = trie.matchAll("abcdefg");
String expected = "[{\"start\":0, \"end\":3, \"key\":\"abcd\", \"value\":\"abcd\"}, {\"start\":1, \"end\":5, \"key\":\"bcdef\", \"value\":\"bcdef\"}]"; Assert.assertEquals(expected, matchAll.toString()); }}
复制代码
4. 对比 StandardTrie
4.1. 时间、空间与动态更新
动态更新:PatriciaTrie 依然支持在查找期间更新数据元素。
时间性能:PatriciaTrie 的增删查依然只跟字符串的长度 m 相关,且其时间复杂度最好和最坏的情况都是 O(m)。
空间性能:减少了单分支节点的创建,但对于稀疏的多分支的情况依然需要创建节点和容量为 R 的数组,依然还是可能存在大量的空间浪费。
4.2. 时间性能对比
这次不再与 HashMap 对比,而是与 StandardTrie 对比。
测试用例不变:使用长度为 10 的固定字符串,循环调用 get 方法 2 亿次,对比两者的时间消耗。
public class PatriciaTrieTest { @Test public void performance() { PatriciaTrie<String> patriciaTrie = new PatriciaTrie<>();
String finalKey = "abcdefghij"; patriciaTrie.put(finalKey, finalKey); StandardTrie<String> standardTrie = new StandardTrie<>(); standardTrie.put(finalKey, finalKey);
// 2亿次 int size = 200000000; long t1 = System.currentTimeMillis(); for (int i = 0; i < size; i++) { patriciaTrie.get(finalKey); }
long t2 = System.currentTimeMillis(); System.out.println("PatriciaTrie-get:\t" + (t2 - t1));
for (int i = 0; i < size; i++) { standardTrie.get(finalKey); }
long t3 = System.currentTimeMillis(); System.out.println("StandardTrie-get:\t" + (t3 - t2)); }}
复制代码
我的电脑上的测试结果:
# 测试平台# CPU:Intel(R) Core(TM) i9-7900X CPU @ 3.30GHz# RAM:64G DDR4(3000 MHz)# OS:Win10(21H1)# JDK:11.0.5
PatriciaTrie-get: 6896StandardTrie-get: 5495
复制代码
对比 StandardTrie,我们发现时间性能略有下降,主要是比较子字符串的逻辑变得更加复杂:节省了空间,却消耗了更多时间,这世上果然没有两全之计啊😀。
不过,2 亿次查询才多耗费了 1 秒多时间,几乎可以忽略不计,相比起可能节约的大量空间,这点时间开销是完全值得的。
5. 总结
Patricia Trie 优化了空间性能,但依然没有完全解决稀疏数据的空间浪费问题——减少了数组的创建,但数组依然可能会有大量的空链接。那么,还有哪些可能的方式来解决这个问题呢?
另外,Standard Trie 和 Patricia Trie,我都采用了字符比较的方式去实现,而原论文都是位比较的方式,那么:
位比较方式是如何推广到字符比较方式的呢?
维基百科中所描述的 Radix Tree 似乎就是 Patricia Trie,两者真的是同一种数据结构吗?如果不是,那么两者究竟有什么关系?
因此,我在下一篇文章中会继续介绍 Patricia Trie——原论文描述的二进制位比较的方式,通过两种实现方式的对比来尝试去解释上面的这些问题。
代码仓库
实验性代码:
Github:https://github.com/patricklaux/perfect-code
Gitee:https://gitee.com/igeeksky/perfect-code
生产级代码:
Github:https://github.com/patricklaux/xtool
Gitee:https://gitee.com/igeeksky/xtool
参考资料
《Algorithms in c, 3ed》[^2] 一书中详细描述了 Patricia Trie 二进制位比较方式的实现,也简单介绍了字符比较方式,有图有代码更易理解,推荐阅读。
《The Art of Computer Programming. Volume III: Sorting and Searching》[^4] 同样介绍了 Patricia Trie 二进制位比较方式的实现,可以与原论文对比阅读。
斯坦福的 cs166 课程[^5]和卡尔顿大学的 Comp5408 课程[^6]也讲解了 Patricia Trie ,这两者的讲解都是基于字符比较的方式。本文代码则是根据这两者的介绍实现(细节略有不同),有兴趣可以查看参考资料 5 和参考资料 6。
NIST[^7] 给出了 Patricia Trie 的名词解释,个人认为比维基百科的词条要准确,见参考资料 7。
[1]: R. Sedgewick and K. Wayne. "Algorithms, fourth edition." Addison-Wesley(2011):730-753
[2]: R. Sedgewick. "Algorithms in C, third edition." Addison-Wesley(1998):614-648
[3]: Morrison, Donald R.. “PATRICIA—Practical Algorithm To Retrieve Information Coded in Alphanumeric.” Journal of the ACM (JACM) 15 (1968): 514 - 534.
[4]: Donald E. Knuth. "The Art of Computer Programming. Volume III: Sorting and Searching." Addison-Wesley(1973):492-512
[5]: http://web.stanford.edu/class/cs166/lectures/16/Slides16.pdf
[6]: https://cglab.ca/~morin/teaching/5408/notes/strings.pdf
[7]: https://xlinux.nist.gov/dads/HTML/patriciatree.html















评论