看一遍就理解:动态规划详解
要想跳到第 10 级台阶,要么是先跳到第 9 级,然后再跳 1 级台阶上去;要么是先跳到第 8 级,然后一次迈 2 级台阶上去。
同理,要想跳到第 9 级台阶,要么是先跳到第 8 级,然后再跳 1 级台阶上去;要么是先跳到第 7 级,然后一次迈 2 级台阶上去。
要想跳到第 8 级台阶,要么是先跳到第 7 级,然后再跳 1 级台阶上去;要么是先跳到第 6 级,然后一次迈 2 级台阶上去。
”
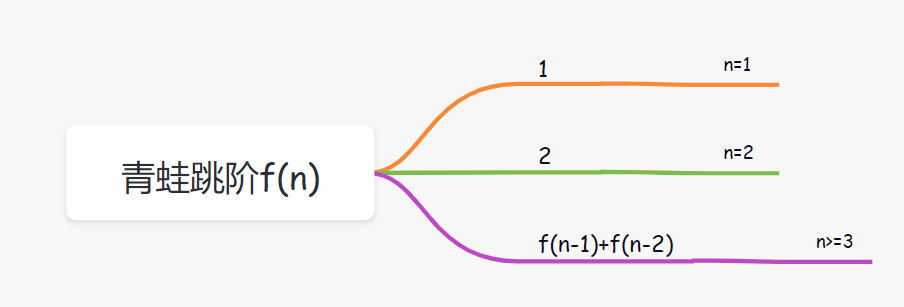
假设跳到第 n 级台阶的跳数我们定义为 f(n),很显然就可以得出以下公式:
f(10)?=?f(9)+f(8)
f?(9)??=?f(8)?+?f(7)
f?(8)??=?f(7)?+?f(6)
...
f(3)?=?f(2)?+?f(1)
即通用公式为:?f(n)?=?f(n-1)?+?f(n-2)
那 f(2) 或者 f(1) 等于多少呢?
当只有 2 级台阶时,有两种跳法,第一种是直接跳两级,第二种是先跳一级,然后再跳一级。即 f(2) = 2;
当只有 1 级台阶时,只有一种跳法,即 f(1)= 1;
因此可以用递归去解决这个问题:
class?Solution?{
public?int?numWays(int?n)?{
if(n?==?1){
return?1;
}
if(n?==?2){
return?2;
}
return?numWays(n-1)?+?numWays(n-2);
}
}
去 leetcode 提交一下,发现有问题,超出时间限制了
为什么超时了呢?递归耗时在哪里呢?先画出递归树看看:
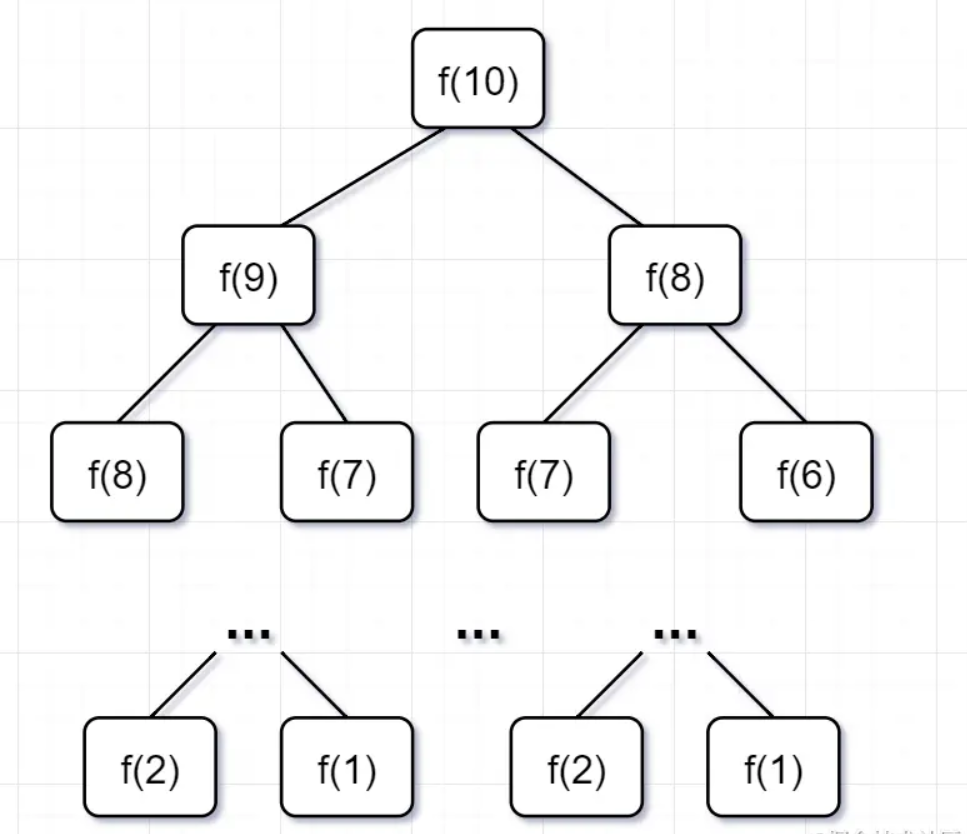
要计算原问题 f(10),就需要先计算出子问题 f(9) 和 f(8)
然后要计算 f(9),又要先算出子问题 f(8) 和 f(7),以此类推。
一直到 f(2) 和 f(1),递归树才终止。
我们先来看看这个递归的时间复杂度吧:
递归时间复杂度?=?解决一个子问题时间*子问题个数
一个子问题时间 = ?f(n-1)+f(n-2),也就是一个加法的操作,所以复杂度是 O(1);
问题个数 = 递归树节点的总数,递归树的总节点 = 2^n-1,所以是复杂度 O(2^n)。
因此,青蛙跳阶,递归解法的时间复杂度 = O(1) * O(2^n) = ?O(2^n),就是指数级别的,爆炸增长的,如果 n 比较大的话,超时很正常的了。
回过头来,你仔细观察这颗递归树,你会发现存在大量重复计算,比如 f(8)被计算了两次,f(7)被重复计算了 3 次...所以这个递归算法低效的原因,就是存在大量的重复计算!
既然存在大量重复计算,那么我们可以先把计算好的答案存下来,即造一个备忘录,等到下次需要的话,先去备忘录查一下,如果有,就直接取就好了,备忘录没有才开始计算,那就可以省去重新重复计算的耗时啦!这就是带备忘录的解法。
带备忘录的递归解法(自顶向下)
一般使用一个数组或者一个哈希 map 充当这个备忘录。
第一步,f(10)= f(9) + f(8),f(9) 和 f(8)都需要计算出来,然后再加到备忘录中,如下:
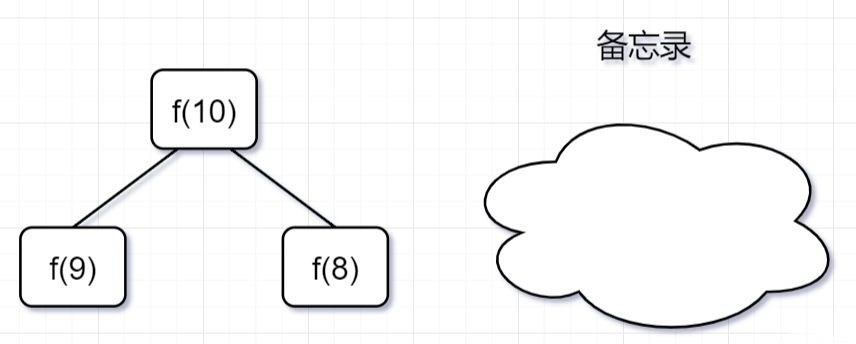
第二步, ?f(9) = f(8)+ f(7),f(8)= f(7)+ f(6), 因为 f(8) 已经在备忘录中啦,所以可以省掉,f(7),f(6)都需要计算出来,加到备忘录中~
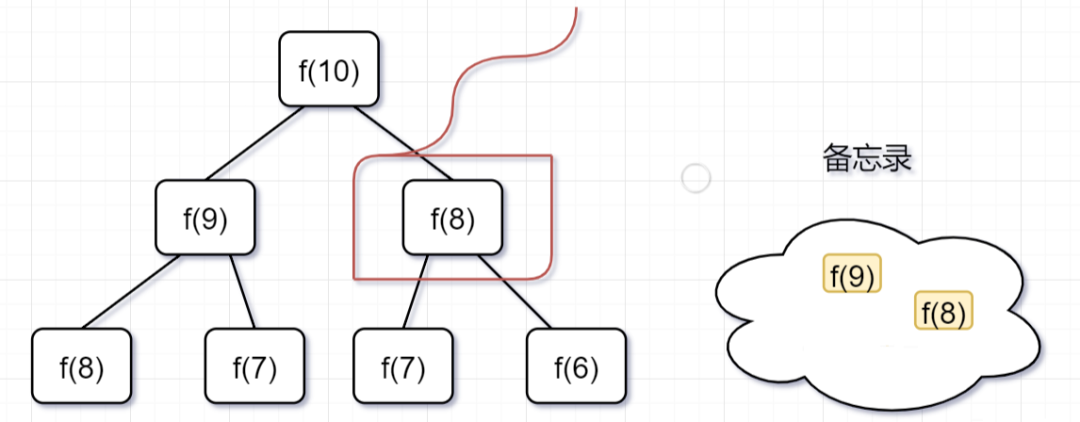
第三步, f(8) = f(7)+ f(6),发现 f(8),f(7),f(6)全部都在备忘录上了,所以都可以剪掉。
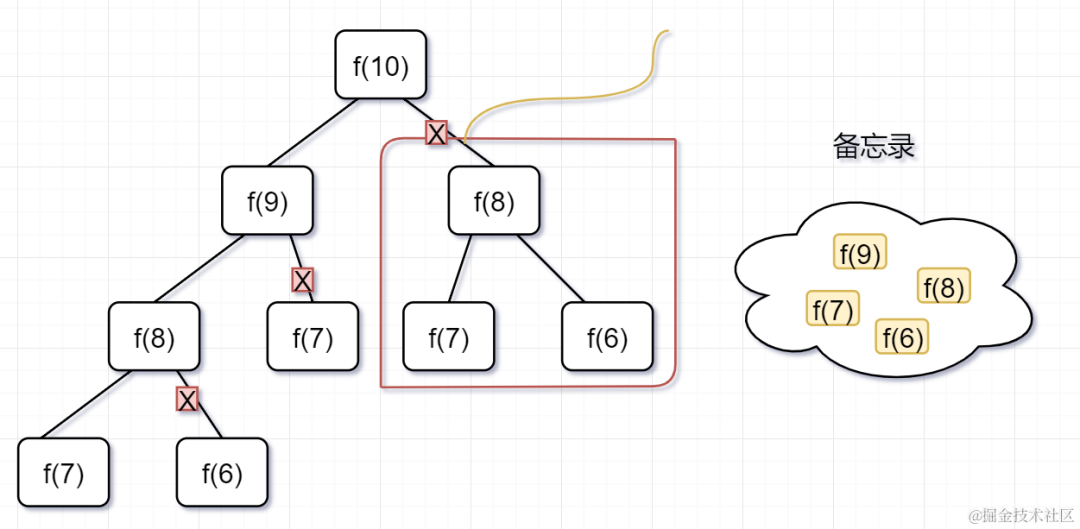
所以呢,用了备忘录递归算法,递归树变成光秃秃的树干咯,如下:
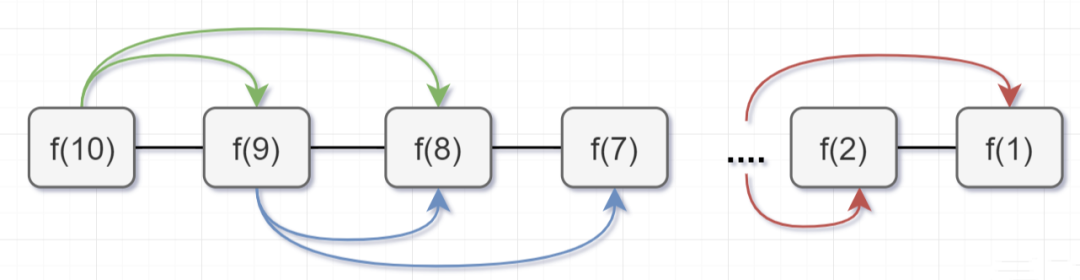
带备忘录的递归算法,子问题个数=树节点数=n,解决一个子问题还是 O(1),所以带备忘录的递归算法的时间复杂度是 O(n)。接下来呢,我们用带备忘录的递归算法去撸代码,解决这个青蛙跳阶问题的超时问题咯~,代码如下:
public?class?Solution?{
//使用哈希 map,充当备忘录的作用
Map<Integer,?Integer>?tempMap?=?new?HashMap();
public?int?numWays(int?n)?{
//?n?=?0?也算 1 种
if?(n?==?0)?{
return?1;
}
if?(n?<=?2)?{
return?n;
}
//先判断有没计算过,即看看备忘录有没有
if?(tempMap.containsKey(n))?{
//备忘录有,即计算过,直接返回
return?tempMap.get(n);
}?else?{
//?备忘录没有,即没有计算过,执行递归计算,并且把结果保存到备忘录 map 中,对 1000000007 取余(这个是 leetcode 题目规定的)
tempMap.put(n,?(numWays(n?-?1)?+?numWays(n?-?2))?%?1000000007);
return?tempMap.get(n);
}
}
}
去 leetcode 提交一下,如图,稳了:
其实,还可以用动态规划解决这道题。
自底向上的动态规划
动态规划跟带备忘录的递归解法基本思想是一致的,都是减少重复计算,时间复杂度也都是差不多。但是呢:
带备忘录的递归,是从 f(10)往 f(1)方向延伸求解的,所以也称为自顶向下的解法。
动态规划从较小问题的解,由交叠性质,逐步决策出较大问题的解,它是从 f(1)往 f(10)方向,往上推求解,所以称为自底向上的解法。
动态规划有几个典型特征,最优子结构、状态转移方程、边界、重叠子问题。在青蛙跳阶问题中:
f(n-1)和 f(n-2) 称为 f(n) 的最优子结构
f(n)= f(n-1)+f(n-2)就称为状态转移方程
f(1) = 1, f(2) = 2 就是边界啦
比如 f(10)= f(9)+f(8),f(9) = f(8) + f(7) ,f(8)就是重叠子问题。
我们来看下自底向上的解法,从 f(1)往 f(10)方向,想想是不是直接一个 for 循环就可以解决啦,如下:
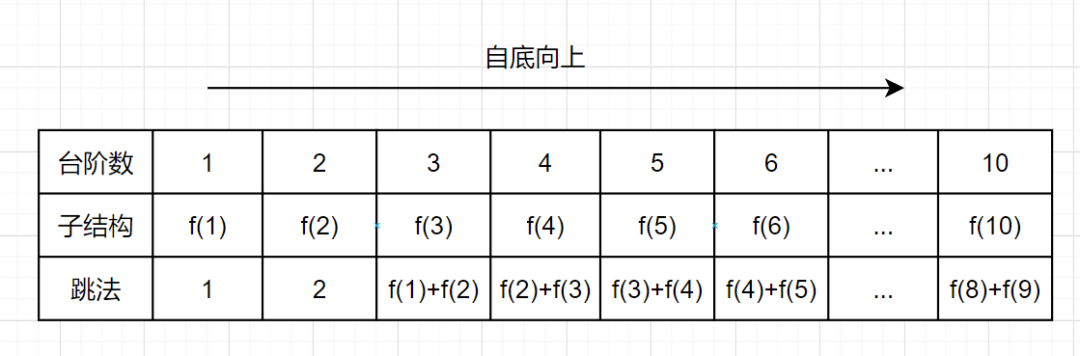
带备忘录的递归解法,空间复杂度是 O(n),但是呢,仔细观察上图,可以发现,f(n)只依赖前面两个数,所以只需要两个变量 a 和 b 来存储,就可以满足需求了,因此空间复杂度是 O(1)就可以啦

动态规划实现代码如下:
public?class?Solution?{
public?int?numWays(int?n)?{
if?(n<=?1)?{
return?1;
}
if?(n?==?2)?{
return?2;
}
int?a?=?1;
int?b?=?2;
int?temp?=?0;
for?(int?i?=?3;?i?<=?n;?i++)?{
temp?=?(a?+?b)%?1000000007;
a?=?b;
b?=?temp;
}
return?temp;
}
}
动态规划的解题套路
什么样的问题可以考虑使用动态规划解决呢?
★
如果一个问题,可以把所有可能的答案穷举出来,并且穷举出来后,发现存在重叠子问题,就可以考虑使用动态规划。
”
比如一些求最值的场景,如最长递增子序列、最小编辑距离、背包问题、凑零钱问题等等,都是动态规划的经典应用场景。
动态规划的解题思路
动态规划的核心思想就是拆分子问题,记住过往,减少重复计算。 并且动态规划一般都是自底向上的,因此到这里,基于青蛙跳阶问题,我总结了一下我做动态规划的思路:
穷举分析
确定边界
找出规律,确定最优子结构
写出状态转移方程
1. 穷举分析
当台阶数是 1 的时候,有一种跳法,f(1) =1
当只有 2 级台阶时,有两种跳法,第一种是直接跳两级,第二种是先跳一级,然后再跳一级。即 f(2) = 2;
当台阶是 3 级时,想跳到第 3 级台阶,要么是先跳到第 2 级,然后再跳 1 级台阶上去,要么是先跳到第 1 级,然后一次迈 2 级台阶上去。所以 f(3) = f(2) + f(1) =3
当台阶是 4 级时,想跳到第 3 级台阶,要么是先跳到第 3 级,然后再跳 1 级台阶上去,要么是先跳到第 2 级,然后一次迈 2 级台阶上去。所以 f(4) = f(3) + f(2) =5
当台阶是 5 级时......

自底向上的动态规划
2. 确定边界
通过穷举分析,我们发现,当台阶数是 1 的时候或者 2 的时候,可以明确知道青蛙跳法。f(1) =1,f(2) = 2,当台阶 n>=3 时,已经呈现出规律 f(3) = f(2) + f(1) =3,因此 f(1) =1,f(2) = 2 就是青蛙跳阶的边界。
3. 找规律,确定最优子结构
n>=3 时,已经呈现出规律 f(n) = f(n-1) + f(n-2) ,因此,f(n-1)和 f(n-2) 称为 f(n) 的最优子结构。什么是最优子结构?有这么一个解释:
★
一道动态规划问题,其实就是一个递推问题。假设当前决策结果是 f(n),则最优子结构就是要让 f(n-k) 最优,最优子结构性质就是能让转移到 n 的状态是最优的,并且与后面的决策没有关系,即让后面的决策安心地使用前面的局部最优解的一种性质
”
4, 写出状态转移方程
通过前面 3 步,穷举分析,确定边界,最优子结构,我们就可以得出状态转移方程啦:
5. 代码实现
我们实现代码的时候,一般注意从底往上遍历哈,然后关注下边界情况,空间复杂度,也就差不多啦。动态规划有个框架的,大家实现的时候,可以考虑适当参考一下:
dp[0][0][...]?=?边界值
for(状态 1 :所有状态 1 的值){
for(状态 2 :所有状态 2 的值){
for(...){
//状态转移方程
dp[状态 1][状态 2][...]?=?求最值
}
}
}
leetcode 案例分析
我们一起来分析一道经典 leetcode 题目吧
★
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
”
示例 1:
输入:nums =?[10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是?[2,3,7,101],因此长度为 4 。
示例 2:
输入:nums =?[0,1,0,3,2,3]
输出:4
我们按照以上动态规划的解题思路,
穷举分析
确定边界
找规律,确定最优子结构
状态转移方程
1.穷举分析
因为动态规划,核心思想包括拆分子问题,记住过往,减少重复计算。 所以我们在思考原问题:数组 num[i]的最长递增子序列长度时,可以思考下相关子问题,比如原问题是否跟子问题 num[i-1]的最长递增子序列长度有关呢?
自底向上的穷举
这里观察规律,显然是有关系的,我们还是遵循动态规划自底向上的原则,基于示例 1 的数据,从数组只有一个元素开始分析。
当 nums 只有一个元素 10 时,最长递增子序列是[10],长度是 1.
当 nums 需要加入一个元素 9 时,最长递增子序列是[10]或者[9],长度是 1。
当 nums 再加入一个元素 2 时,最长递增子序列是[10]或者[9]或者[2],长度是 1。
当 nums 再加入一个元素 5 时,最长递增子序列是[2,5],长度是 2。
当 nums 再加入一个元素 3 时,最长递增子序列是[2,5]或者[2,3],长度是 2。
当 nums 再加入一个元素 7 时,,最长递增子序列是[2,5,7]或者[2,3,7],长度是 3。
当 nums 再加入一个元素 101 时,最长递增子序列是[2,5,7,101]或者[2,3,7,101],长度是 4。
当 nums 再加入一个元素 18 时,最长递增子序列是[2,5,7,101]或者[2,3,7,101]或者[2,5,7,18]或者[2,3,7,18],长度是 4。
当 nums 再加入一个元素 7 时,最长递增子序列是[2,5,7,101]或者[2,3,7,101]或者[2,5,7,18]或者[2,3,7,18],长度是 4.
分析找规律,拆分子问题
通过上面分析,我们可以发现一个规律:
如果新加入一个元素 nums[i], 最长递增子序列要么是以 nums[i]结尾的递增子序列,要么就是 nums[i-1]的最长递增子序列。看到这个,是不是很开心,nums[i]的最长递增子序列已经跟子问题 nums[i-1]的最长递增子序列有关联了。
原问题数组 nums[i]的最长递增子序列?=?子问题数组 nums[i-1]的最长递增子序列/nums[i]结尾的最长递增子序列
是不是感觉成功了一半呢?但是如何把 nums[i]结尾的递增子序列也转化为对应的子问题呢?要是 nums[i]结尾的递增子序列也跟 nums[i-1]的最长递增子序列有关就好了。又或者 nums[i]结尾的最长递增子序列,跟前面子问题 num[j](0=<j<i)结尾的最长递增子序列有关就好了,带着这个想法,我们又回头看看穷举的过程:

nums[i]的最长递增子序列,不就是从以数组 num[i]每个元素结尾的最长子序列集合,取元素最多(也就是长度最长)那个嘛,所以原问题,我们转化成求出以数组 nums 每个元素结尾的最长子序列集合,再取最大值嘛。哈哈,想到这,我们就可以用 dp[i]表示以 num[i]这个数结尾的最长递增子序列的长度啦,然后再来看看其中的规律:
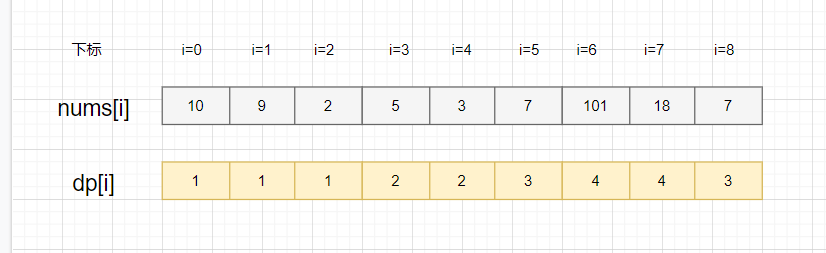
其实,nums[i]结尾的自增子序列,只要找到比 nums[i]小的子序列,加上 nums[i] 就可以啦。显然,可能形成多种新的子序列,我们选最长那个,就是 dp[i]的值啦
★
nums[3]=5,以
5结尾的最长子序列就是[2,5],因为从数组下标0到3遍历,只找到了子序列[2]比5小,所以就是[2]+[5]啦,即dp[4]=2
nums[4]=3,以
3结尾的最长子序列就是[2,3],因为从数组下标0到4遍历,只找到了子序列[2]比3小,所以就是[2]+[3]啦,即dp[4]=2
nums[5]=7,以
7结尾的最长子序列就是[2,5,7]和[2,3,7],因为从数组下标0到5遍历,找到2,5和3都比 7 小,所以就有[2,7],[5,7],[3,7],[2,5,7]和[2,3,7]这些子序列,最长子序列就是[2,5,7]和[2,3,7],它俩不就是以5结尾和3结尾的最长递增子序列+[7]来的嘛!所以,dp[5]=3 =dp[3]+1=dp[4]+1。
”
很显然有这个规律:一个以 nums[i]结尾的数组 nums
如果存在 j 属于区间[0,i-1],并且 num[i]>num[j]的话,则有:
dp(i) =max(dp(j))+1,
最简单的边界情况
当 nums 数组只有一个元素时,最长递增子序列的长度 dp(1)=1,当 nums 数组有两个元素时,dp(2) =2 或者 1, 因此边界就是 dp(1)=1。
确定最优子结构
从穷举分析,我们可以得出,以下的最优结构:
dp(i)?=max(dp(j))+1,存在 j 属于区间[0,i-1],并且 num[i]>num[j]。
max(dp(j)) 就是最优子结构。









评论