智力题（BAT 面试经典题），vue 数据双向绑定

2021 年 11 月 28 日
本文字数：2776 字
阅读完需：约 9 分钟

乍一看，似乎是可以盖住的。棋盘大小为 8×8，共有 64 个方格，但其中两个方格已被切掉，因此只剩 62 个方格。31 块骨牌应该刚好能盖住整个棋盘，对吧？

尝试用骨牌盖住第 1 行，而第 1 行只有 7 个方格，因此有一块骨牌必须铺至第 2 行。而用骨牌盖住第 2 行时，我们又必须将一块骨牌铺至第 3 行。

要盖住每一行，总有一块骨牌必须铺至下一行。无论尝试多少次、多少种方法，我们都无法成功铺下所有骨牌。

其实，还有更简洁更严谨的证明说明为什么不可能。棋盘原本有 32 个黑格和 32 个白格。将对角角落上的两个方格（相同颜色）切掉，棋盘只剩下 30 个同色的方格和 32 个另一种颜色的方格。为方便论证起见，我们假定棋盘上剩下 30 个黑格和 32 个白格。

放在棋盘上的每块骨牌必定会盖住一个白格和一个黑格。因此，31 块骨牌正好盖住 31 个白格和 31 个黑格。然而，这个棋盘只有 30 个黑格和 32 个白格，所以，31 块骨牌盖不住整个棋盘。

NO.3

有两个水壶，容量分别为 5 夸脱（美制：1 夸脱=0.946 升，英制：1 夸脱=1.136 升）和 3 夸脱，若水的供应不限量（但没有量杯），怎么用这两个水壶得到刚好 4 夸脱的水？注意，这两个水壶呈不规则形状，无法精准地装满“半壶”水。

解法；根据题意，我们只能使用这两个水壶，不妨随意把玩一番，把水倒来倒去，可以得到如下顺序组合：

注意，许多智力题其实都隐含数学或计算机科学的背景，这个问题也不例外。只要这两个水壶的容量互质（即两个数没有共同的质因子），我们就能找出一种倒水的顺序组合，量出 1 到 2 个水壶容量总和（含）之间的任意水量。

NO.4

有个岛上住着一群人，有一天来了个游客，定了一条奇怪的规矩：所有蓝眼睛的人都必须尽快离开这个岛。每晚 8 点会有一个航班离岛。每个人都看得见别人眼睛的颜色，但不知道自己的（别人也不可以告知）。此外，他们不知道岛上到底有多少人是蓝眼睛的，只知道至少有一个人的眼睛是蓝色的。所有蓝眼睛的人要花几天才能离开这个岛？

解法；下面将采用简单构造法。假定这个岛上一共有 n 人，其中 c 人有蓝眼睛。由题目可知，c > 0。

情况 c = 1：只有一人是蓝眼睛的假设岛上所有人都是聪明的，蓝眼睛的人四处观察之后，发现没有人是蓝眼睛的。但他知道至少有一人是蓝眼睛的，于是就能推导出自己一定是蓝眼睛的。因此，他会搭乘当晚的飞机离开。

情况 c = 2：只有两人是蓝眼睛的两个蓝眼睛的人看到对方，并不确定 c 是 1 还是 2，但是由上一种情况，他们知道，如果 c = 1，那个蓝眼睛的人第一晚就会离岛。因此，发现另一个蓝眼睛的人仍在岛上，他一定能推断出 c = 2，也就意味着他自己也是蓝眼睛的。于是，两个蓝眼睛的人都会在第二晚离岛。

情况 c > 2：一般情况逐步提高 c 时，我们可以看出上述逻辑仍旧适用。如果 c = 3，那么，这三个人会立即意识到有 2 到 3 人是蓝眼睛的。如果有两人是蓝眼睛的，那么这两人会在第二晚离岛。因此，如果过了第二晚另外两人还在岛上，每个蓝眼睛的人都能推断出 c = 3，因此这三人都有蓝眼睛。他们会在第三晚离岛。

不论 c 为什么值，都可以套用这个模式。所以，如果有 c 人是蓝眼睛的，则所有蓝眼睛的人要用 c 晚才能离岛，且都在同一晚离开。

NO.5

有栋建筑物高 100 层。若从第 N 层或更高的楼层扔下来，鸡蛋就会破掉。若从第 N 层以下的楼层扔下来则不会破掉。给你 2 个鸡蛋，请找出 N，并要求最差情况下扔鸡蛋的次数为最少。（这样问会不会好最少试验多少次可以找出鸡蛋不会被摔碎的最高楼层？）

解法；我们发现，无论怎么扔鸡蛋 1（Egg 1），鸡蛋 2（Egg 2）都必须在“破掉那一层”和下一个不会破掉的最高楼层之间，逐层扔下楼（从最低的到最高的）。

例如，若鸡蛋 1 从 5 层和 10 层楼扔下没破掉，但从 15 层扔下时破掉了，那么，在最差情况下，鸡蛋 2 必须尝试从 11、12、13 和 14 层扔下楼。

具体做法；首先，让我们试着从 10 层开始扔鸡蛋，然后是 20 层，等等。如果鸡蛋 1 第一次扔下楼（10 层）就破掉了，那么，最多需要扔 10 次。如果鸡蛋 1 最后一次扔下楼（100 层）才破掉，那么，最多要扔 19 次（10、20、…、90、100 层，然后是 91 到 99 层）。这么做也挺不错，但我们只考虑了绝对最差情况。我们应该进行“负载均衡”，让这两种情况下扔鸡蛋的次数更均匀。我们的目标是设计一种扔鸡蛋的方法，使得扔鸡蛋 1 时，不论是在第一次还是最后一次扔下楼才破掉，次数越稳定越好。

(1) 完美负载均衡的方法应该是，扔鸡蛋 1 的次数加上扔鸡蛋 2 的次数，不论什么时候都一样，不管鸡蛋 1 是从哪层楼扔下时破掉的。(2) 若有这种扔法，每次鸡蛋 1 多扔一次，鸡蛋 2 就可以少扔一次。(3) 因此，每丢一次鸡蛋 1，就应该减少鸡蛋 2 可能需要扔下楼的次数。例如，如果鸡蛋 1 先从 20 层往下扔（不破），然后从 30 层扔下楼（破），此时鸡蛋 2 可能就要扔 9 次（从 21 到 29 一次次试）。若鸡蛋 1 再扔一次，我们必须让鸡蛋 2 扔下楼的次数降为 8 次。也就是说，我们必须让鸡蛋 1 从 39 层扔下楼。(4) 由此可知，鸡蛋 1 必须从 X 层开始往下扔，然后再往上增加 X-1 层……直至到达 100 层。 (5) 求解方程式 X + (X-1) + (X-2) + … + 1 = 100，得到 X (X + 1) / 2 = 100 → X = 14。（直接设要 X 次，假如 X 和 X-1 这两次了则再加 X-2 总共还是 X 次，次数总为 X）我们先从 14 层开始，然后是 27 层，

《Android 学习笔记总结+最新移动架构视频+大厂安卓面试真题+项目实战源码讲义》
【docs.qq.com/doc/DSkNLaERkbnFoS0ZF】完整内容开源分享

接着是 39 层，依此类推，最差情况下鸡蛋要扔 14 次。正如解决其他许多最大化/最小化的问题一样，这类问题的关键在于“平衡最差情况”。

NO.6

走廊上有 100 个关上的储物柜。有个人先是将 100 个柜子全都打开。接着，每数两个柜子关上一个。然后，在第三轮时，再每隔两个就切换第三个柜子的开关状态（也就是将关上的柜子打开，将打开的关上）。照此规律反复操作 100 次，在第 i 轮，这个人会每数 i 个就切换第 i 个柜子的状态。当第 100 轮经过走廊时，只切换第 100 个柜子的开关状态，此时有几个柜子是开着的？

解法；要解决这个问题，我们必须弄清楚所谓切换储物柜开关状态是什么意思。这有助于我们推断最终哪些柜子是开着的。

问题：柜子会在哪几轮切换状态（开或关）？柜子 n 会在 n 的每个因子（包括 1 和 n 本身）对应的那一轮切换状态。也就是说，柜子 15 会在第 1、3、5 和 15 轮开或关一次。（i=1 开，3 关，5 开，15 关。因子个数：偶数关，奇数开）
问题：柜子什么时候还是开着的？如果因子个数（记作 x）为奇数，则这个柜子是开着的。你可以把一对因子比作开和关，若还剩一个因子，则柜子就是开着的。

文末

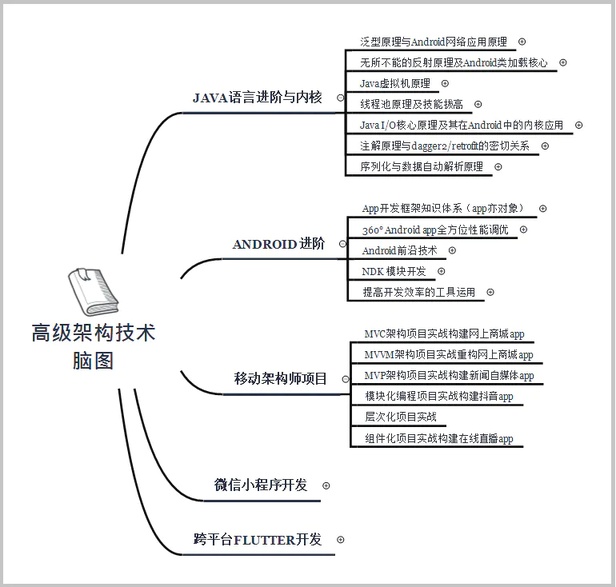
架构师不是天生的，是在项目中磨练起来的，所以，我们学了技术就需要结合项目进行实战训练，那么在 Android 里面最常用的架构无外乎 MVC，MVP，MVVM，但是这些思想如果和模块化，层次化，组件化混和在一起，那就不是一件那么简单的事了，我们需要一个真正身经百战的架构师才能讲解透彻其中蕴含的深理。