Android 贝塞尔曲线实战之网易云音乐鲸云特效，kotlin 教程 pdf

APP 开发市场已经告别“野蛮生长”时代，人们不再满足于 APP 外形创新，而将目光转向全方面的用户体验上。在这过程中，动效化作为移动互联网产品的新趋势，如何实现酷炫丝滑的动画效果已然成为开发者们的新课题。实现方式其实很简单。本文将为你剖析理论基础以及具体应用。看完这篇文章，你的 App 也可以达到酷炫吊炸天的动画效果。

先看两个例子：

1. 手机 QQ 未读消息红点拖拽效果。

2. 小说阅读 APP 的翻页效果。

简介

=====================================================================

在开始实战之前，我们还是先了解下理论基础。动画的终极武器就是贝塞尔曲线了。它是一条光滑的曲线，依据四个位置任意的点坐标绘制而成。1962 年，法国工程师皮埃尔·贝塞尔（Pierre Bézier）率先研究出这种矢量绘制曲线的方法并给出了详细的计算公式，应用于汽车的主体设计。因此，人们将按照此种公式绘制的曲线命名为贝塞尔曲线。

核心思想

贝塞尔曲线是计算机图形学中运用得最多的参数曲线之一。它通过控制曲线上的四个点（起始点、终止点以及两个相互分离的中间点）来创造、编辑图形。其中起重要作用的是位于曲线中央的控制线。这条线是虚拟的，中间与贝塞尔曲线交叉，两端是控制端点。移动两端的端点时贝塞尔曲线可以改变曲线的曲率（弯曲的程度）；移动中间点（也就是移动虚拟的控制线）时，贝塞尔曲线在起始点和终止点锁定的情况下做均匀移动。注意：贝塞尔曲线上的所有控制点、节点均可编辑。

原理

这里面有个通用公式，这个公式已经有前辈帮我们总结好了。

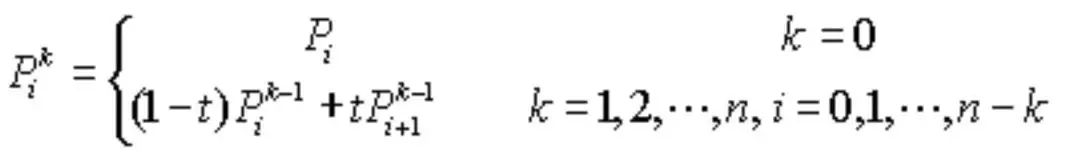
其中 P0 为起点，Pn 为中点，Pi 为控制点。

一阶贝塞尔曲线

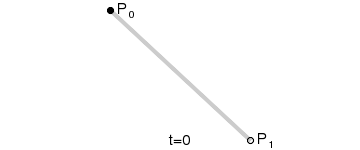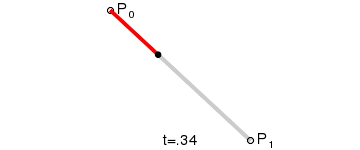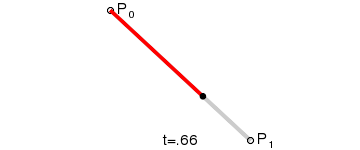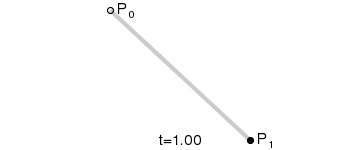
一阶这个比较简单，因为没有在网上找到可以直接输入数学公式的工具，就手工推导了下。

最后的公式为 B(t)=(1-t)Po+tP1,t->[0,1]

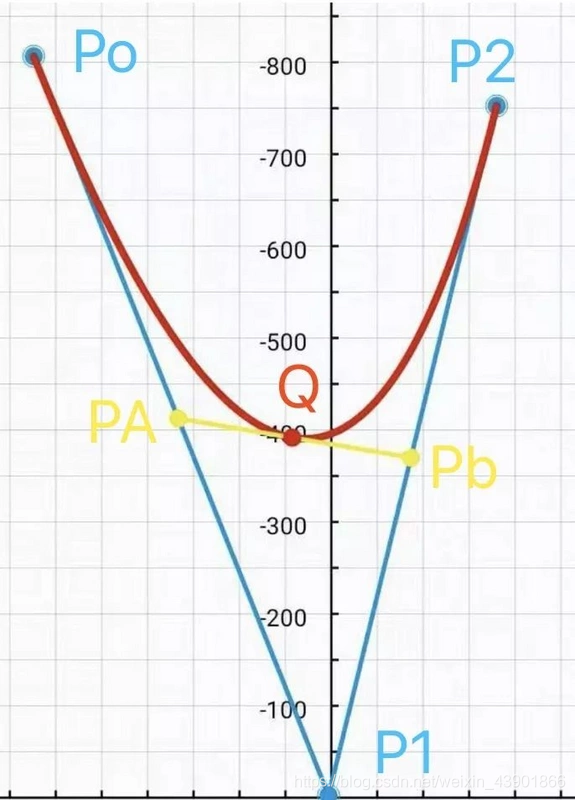
二阶贝塞尔曲线

先看动画效果。

关注红线部分，这条线就是我们单位时间内运行的贝塞尔曲线效果图。这条红线实际上是由无数个点组成，随着 t 的不断变化，红线的转换过程非常的顺滑。

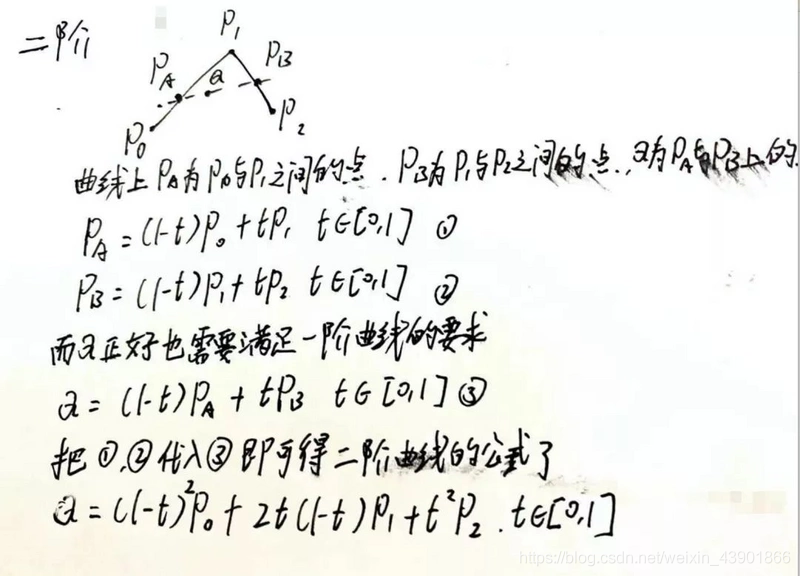
最后得到的公式如下：

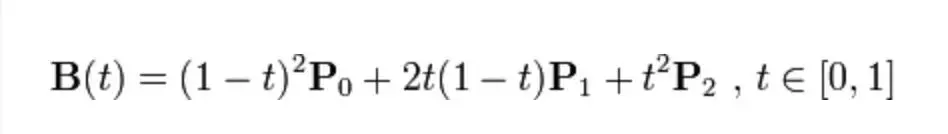
贝塞尔曲线的绘制，无论多少阶（一阶除外），均需要逐级降阶，最终降至一阶。在 “二阶贝塞尔曲线解析” 这段文字中，从 第一步 到 第二步 的过程就是在降阶。贝塞尔曲线最终的路径是由 一阶基线 上游走的红色小点形成的。

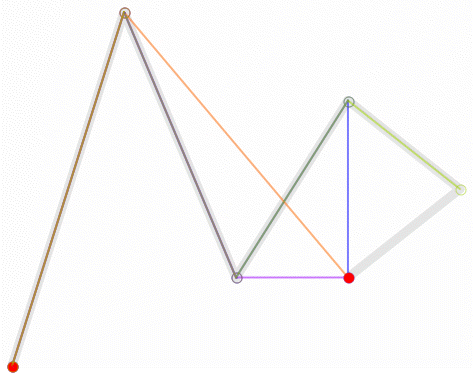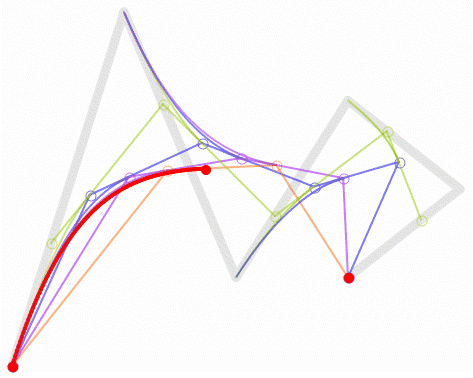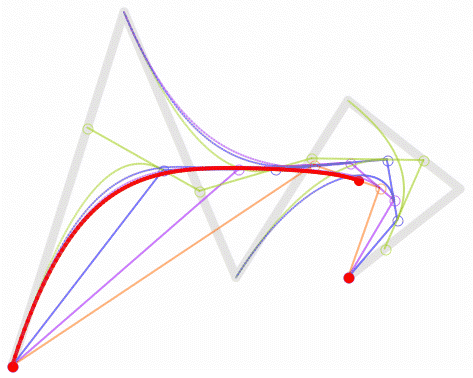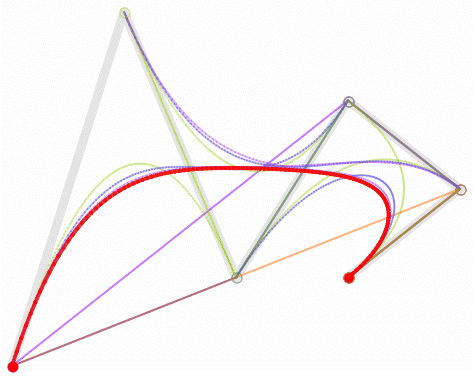
三阶贝塞尔曲线

有了二阶的推导过程，三阶的推导就容易多啦。由于篇幅限制，推导过程这里不再展开，大家有兴趣的话可以自行推导下。

最后的红色曲线是由蓝色一阶曲线获得的，而蓝色一阶曲线又是由绿色一阶曲线获得，最后的绿色一阶曲线则是最外的 P0,P1,P2,P3 构成的。动画效果为：

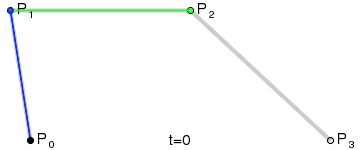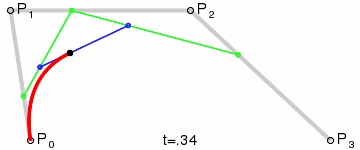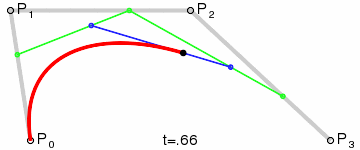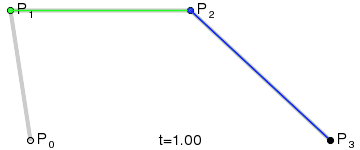
四阶贝塞尔曲线

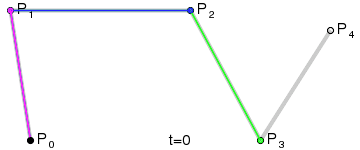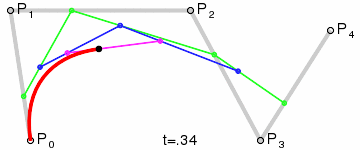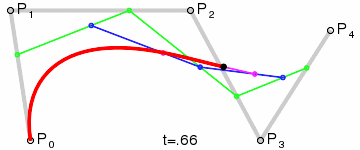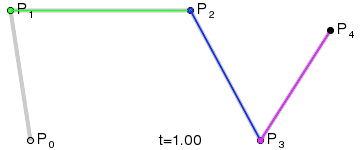
五阶贝塞尔曲线

结论我们发现原来贝塞尔曲线上的点与高数中二项式展开一样，对于每个线段上的点经过控制点进行切面操作，而连续的两点之间是无限接近的，所以在绘制的过程中会出现非常丝滑地过度。

贝塞尔曲线在 Android 上的使用

在 Android 中使用贝塞尔曲线比较简单，Android 已经内置了贝塞尔曲线的 API，开发者可以直接予以调用。主要有两个 API 。

quadTo

Path path = new Path(); path.moveTo(startX, startY);

path.quadTo(eventX, eventY, endX, endY);

canvas.drawPath(path, paint);

其中 （startX，startY） 为起点，（endX，endY）为终点，而 （eventX，eventY）即为控制点了。

cubicTo

Path path = new Path();

path.moveTo(startX, startY);

path.cubicTo(leftX, leftY, rightX, rightY, endX, endY);

canvas.drawPath(path, paint);

调用此方法即可画出一条三阶贝塞尔曲线。（startX，startY）为起点，（endX，endY）为终点，而（leftX，leftY）与(rightX，rightY) 为两个控制点了。

多阶贝塞尔曲线：Android 系统最高只能画出三阶的贝塞尔曲线，那么想画出更高阶的怎么办呢？其实也很简单。如果真的需要使用高阶的曲线，可以进行人工降阶，降阶到 3 级即可。

实战

============================

《Android 学习笔记总结+最新移动架构视频+大厂安卓面试真题+项目实战源码讲义》

【docs.qq.com/doc/DSkNLaERkbnFoS0ZF】 完整内容开源分享

=========================================

终于到实战环节了，该环节共有两个 demo。一个是贝塞尔曲线拟圆效果，另一个是仿网易云音乐里面的鲸云效果。

效果实现 1：以贝塞尔曲线画圆为例

前文总结了贝塞尔曲线的通用公式。在网上浏览资料的过程中我们发现有这么一个公式：(4/3)tan(π/(2n))，其意义是由 n 段三阶贝塞尔曲线拟合圆形时，曲线端点到该端点最近的控制点的最佳距离是(4/3)tan(π/(2n))。大家感兴趣的话可以自行推导。推导过程并不复杂，因为贝塞尔曲线有个重要的性质，即曲线方程中 t=0.5 时的点一定落在圆弧上。只需要把坐标系带入到三阶方程式即可。

最后得知当 t=0.5，根据圆形方程式 X2+Y2=R^2 ，得到 h=(4/3)(sqrt(2)-1) ≈ 0.552284749831 。有了上述的理论基础，再去画圆就非常的轻松，我们先在草稿纸中得到这么一个模型。

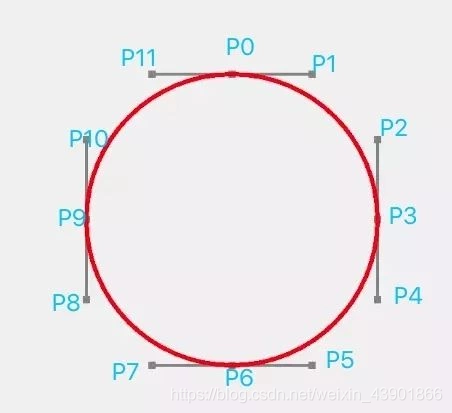
根据上图，这个圆是由 4 段三阶贝塞尔曲线构成的，分别是 P0->P3，P3->P6，P6->P9，P9->P11。三阶贝塞尔曲线的构图是 Android 内置的，我们直接调用 API 即可，核心代码如下：

public HeartView(Context context, @Nullable AttributeSet attrs, int defStyleAttr) {

super(context, attrs, defStyleAttr);

init(context)

}

@Override

protected void init(Context context) {

mPaint = new Paint();

mPaint.setAntiAlias(true);

mPaint.setColor(Color.RED);

mPaint.setStyle(Paint.Style.FILL);

mPath = new Path();

//绘制 12 个点。

mCurPointList = new ArrayList<>();

mCurPointList.add(new PointF(0, dpToPx(-89)));

mCurPointList.add(new PointF(dpToPx(50), dpToPx(-89)));

mCurPointList.add(new PointF(dpToPx(90), dpToPx(-49)));

mCurPointList.add(new PointF(dpToPx(90), 0));

mCurPointList.add(new PointF(dpToPx(90), dpToPx(50)));

mCurPointList.add(new PointF(dpToPx(50), dpToPx(90)));

mCurPointList.add(new PointF(0, dpToPx(90)));

mCurPointList.add(new PointF(dpToPx(-49), dpToPx(90)));

mCurPointList.add(new PointF(dpToPx(-89), dpToPx(50)));

mCurPointList.add(new PointF(dpToPx(-89), 0));

mCurPointList.add(new PointF(dpToPx(-89), dpToPx(-49)));

mCurPointList.add(new PointF(dpToPx(-49), dpToPx(-89)));

}

@Override

protected void onDraw(Canvas canvas) {

drawCoordinate(canvas);

canvas.translate(mWidth / 2, mHeight / 2);

mPath.reset();

for (int i = 0; i < 4; i++) {

if (i == 0) {

mPath.moveTo(mCurPointList.get(i * 3).x, mCurPointList.get(i * 3).y);

} else {

mPath.lineTo(mCurPointList.get(i * 3).x, mCurPointList.get(i * 3).y);

}

int endPointIndex;

if (i == 3) {

endPointIndex = 0;

} else {

endPointIndex = i * 3 + 3;

}

mPath.cubicTo(mCurPointList.get(i * 3 + 1).x, mCurPointList.get(i * 3 + 1).y,

mCurPointList.get(i * 3 + 2).x, mCurPointList.get(i * 3 + 2).y,

mCurPointList.get(endPointIndex).x, mCurPointList.get(endPointIndex).y);

}

canvas.drawPath(mPath, mPaint);

}

}成果展示

效果实现 2：以网易云音乐鲸云效果为例

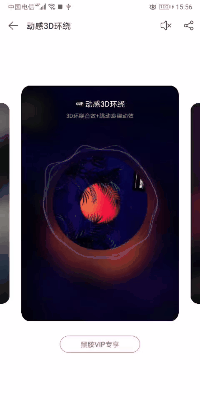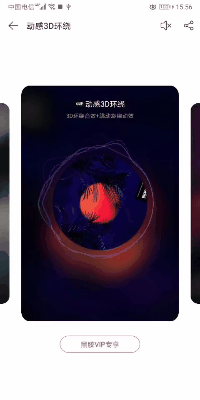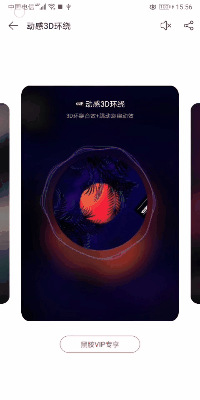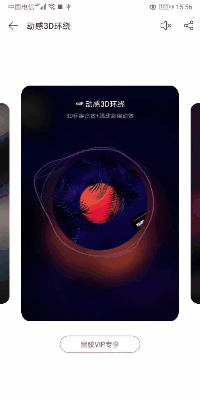
转换成 GIF，图片可能会有点失真，但并不妨碍具体实现思路。根据这个 GIF，我们发现有三点功能需要去完成：

1.背景色与歌曲图片相搭配，随图片的变化而变化；

2.歌曲中间图片是一张圆形图片并且可以自动旋转；

3.图形外圈有动感 3D 环绕效果。

文末

面试：如果不准备充分的面试，完全是浪费时间，更是对自己的不负责！

不管怎么样，不论是什么样的大小面试，要想不被面试官虐的不要不要的，只有刷爆面试题题做好全面的准备，当然除了这个还需要在平时把自己的基础打扎实，这样不论面试官怎么样一个知识点里往死里凿，你也能应付如流啊

本文已被CODING开源项目：《Android学习笔记总结+移动架构视频+大厂面试真题+项目实战源码》收录