【算法社区】训练准备和复杂度分析

​​前言：📫 作者简介：小明java问道之路，专注于研究计算机底层的博主，就职于金融公司后端高级工程师，擅长交易领域的高安全/可用/并发/性能的设计和架构📫 🏆 Java 领域新星创作者、阿里云专家博主、华为云享专家🏆🔥 如果此文还不错的话，还请👍关注、点赞、收藏三连支持👍一下博主哦

本文导读：本文介绍了学习算法和数据结构的方法和准备工作，介绍了学习算法的一些必要的专业名词，时间复杂度、空间复杂度的代码案例

一、训练准备-怎么学？学到什么程度？

1、怎么学？第一遍：读题和思考 5-15 分钟，如果有思路的话自己开始做和写代码（思考所有的可能解法）；如果没思路看题解，前提是读题思考 15 分钟（理解题目的意思），看题解默写背诵（思考所有的可能解法）、熟练（分析每种解法的思路），然后开始自己写（闭卷）第二遍：默写程序、调试（先在头脑里面调试，实在不行再在编译器里调试），这一遍一定要弄会，会写，哪怕时间长（刻意练习、分解—构建知识树、知识模型）第三遍：隔一天再写一遍程序，思考那里写错了，为了记忆第四遍：一周后再写一遍，思考和其他的知识模型的关联，建立知识模型！第五遍：面试前写一遍，复习

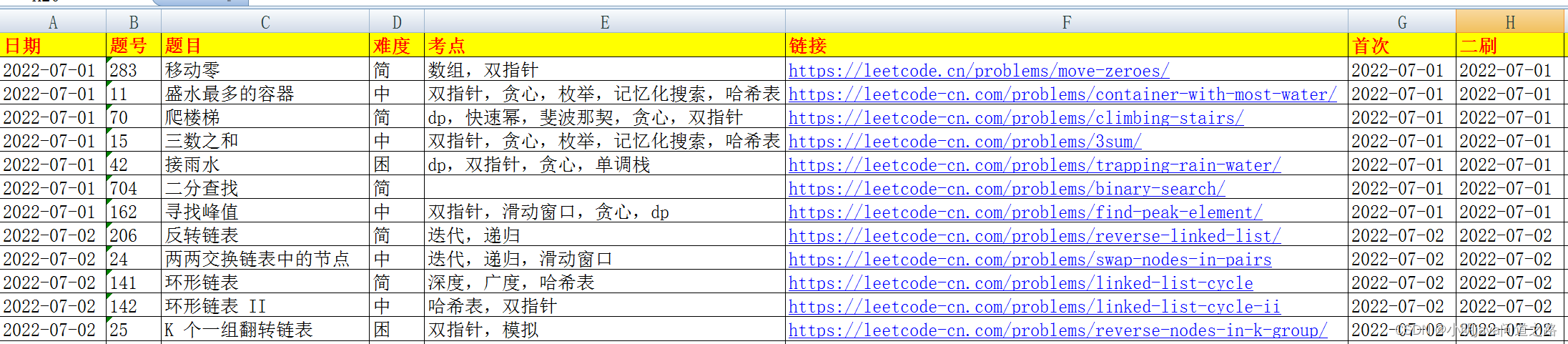
2、学到什么程度？

可以构件知识树（知识模型、思维导图），做过的题有多种解法，讲出来举一反三

二、复杂度原理衡量代码的好坏，包括两个非常重要的指标：

1.运行时间；2.占用空间。衡量标准有个度就是时间复杂度和空间复杂度

时间复杂度：算法的时间复杂度表示为，若存在函数 f（n），使得当 n 趋近于无穷大时，T（n）/ f（n）的极限值为不等于零的常数，则称 f（n）是 T（n）的同数量级函数。记作 T（n）= O（f（n）），称 O（f（n）） 为算法的渐进时间复杂度，简称时间复杂度。

空间复杂度：算法的空间复杂度通过计算算法所需的存储空间实现，算法空间复杂度的计算公式记作：S(n)=O(f(n))，其中，n 为问题的规模，f(n)为语句关于 n 所占存储空间的函数。

如何推导出时间复杂度呢，有如下几个原则：1、如果运行时间是常数量级，用常数 1 表示；2、只保留时间函数中的最高阶项；3、如果最高阶项存在，则省去最高阶项前面的系数。

如何影响空间复杂度的三个方面：一个算法在计算机存储器上所占用的存储空间，包括 1、存储算法本身所占用的存储空间 2、算法的输入输出数据所占用的存储空间 3、算法在运行过程中临时占用的存储空间

三、复杂度算法分析

（一）几种时间复杂度的代码示例

O(1) 算法

一种算法的运算次数与数据规模无关，那么它的时间复杂度是常数级别的，写成 O(1)，哈希算法就是典型的 O(1)时间复杂度，无论数据规模多大，都可以在一次计算后找到目标。

int fun(int key) {    return -key;}

O(logn) 算法

时间复杂度 O(logn)对数阶，当数据增大 n 倍时，耗时增大 logn 倍，二分查找就是 O(logn)的算法，每次排除一半的可能

int fun(int a[], int key) {    int low = 0;    int high = a.length - 1;    while (low <= high) {        int mid = low + (high - low) / 2;        if (a[mid] > key) high = mid - 1;        else if (a[mid] < key) low = mid + 1;        else return mid;    }    return -1;}

O(n) 算法

线性阶，就代表数据量增大几倍，耗时也增大几倍，比如常见的遍历算法

void fun(int i) {    for (int a = 0; a < i; a++)}

O(nlogn)算法

线性对数，就是 n 乘以 logn（遍历的同时内部可以排除一半数据），当数据增大 256，耗时增大 256*8=2048 倍。这个复杂度高于线性低于平方。归并排序就是 O(nlogn)的时间复杂度。

public void mergeSort(int[] arr, int p, int q) {    if (p >= q) return;    int mid = (p + q) / 2;    mergeSort(arr, p, mid);    mergeSort(arr, mid + 1, q);    merge(arr, p, mid, q);}
private void merge(int[] arr, int p, int mid, int q) {    int[] temp = new int[arr.length];    int i = p, j = mid + 1, iter = p;    while (i <= mid && j <= q) {        if (arr[i] <= arr[j]) temp[iter++] = arr[i++];        else temp[iter++] = arr[j++];    }    while (i <= mid) {        temp[iter++] = arr[i++];    }    while (j <= q) {        temp[iter++] = arr[j++];    }    for (int t = p; t <= q; t++) arr[t] = temp[t];}

O(n²)算法

void fun(int i) {    for (int a = 0; a < i; a++)        for (int b = a; a < i; a++)}

对比 O(n³) 算法、 O(n²)算法、O(nlogn) 算法、O(n) 算法、O(logn) 算法

​

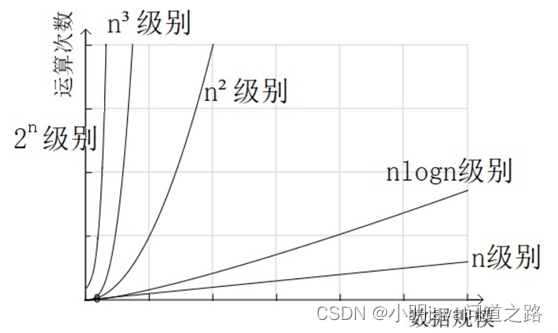
​编辑​

（二）几种空间复杂度的代码示例

常量空间

类似于时间复杂度 O(1)，当算法的存储空间大小固定，和输入规模没有直接的关系时，空间复杂度记作 O(1)

int a = 0;

线性空间

当算法分配的空间是一个线性的集合（如数组），并且集合大小和输入规模 n 成正比时，空间复杂度记作 O(n)

int[] a = new int[n];

二维空间

当算法分配的空间是一个二维数组集合，并且集合的长度和宽度都与输入规模 n 成正比时，空间复杂度记作 O(n^2)

int[][] arr = new int[i][j];

递归空间

在操作系统执行程序时，会专门分配一块内存，用来存储“方法调用栈”。此时栈空间复杂度就是 O(n)。方法调用栈包括入栈和出栈两个操作：当进入一个新方法时，执行入栈操作，把调用的方法和参数信息压入栈中。当方法返回时，执行出栈操作，把调用的方法和参数信息从栈中弹出

void fun(int i) {    fun(i);}

小结：本文介绍了学习算法和数据结构的方法和准备工作，介绍了学习算法的一些必要的专业名词等等