随机数是专门的随机实验的结果，在统计学的不同技术中需要使用随机数，比如在从统计总体中抽取有代表性的样本的时候，或者在将实验动物分配到不同的实验组的过程中，或许在进行蒙特卡罗模拟法计算的时候等等。产生随机数有多种不同的方法，这些方法被称为随机数发生器。随机数量重要的特性是：他所产生的后面的那个数与前面的那个数毫无联系。

今天我们讨论的问题就是基于随机数展开的。总所周知，彩票就是一种随机的发生，但是在这随机的表面下实际上是一种有目的行的控制的随机。简而言之是在大概率下的随机生成

定义概率集改造概率集随机生成概率集索引通过率索查找元素测试数据验证加入战队

目录

[TOC]

<span id="definition">定义概率集</span>

/** * 定义一个连续集合 * 集合中元素x满足:(minElement,maxElement] * 数学表达式为：minElement < x <= maxElement * */public class ContinuousList {
    private double minElement;    private double maxElement;
    public ContinuousList(double minElement, double maxElement){        if(minElement > maxElement){            throw new IllegalArgumentException("区间不合理，minElement不能大于maxElement！");        }        this.minElement = minElement;        this.maxElement = maxElement;    }
    /**     * 判断当前集合是否包含特定元素     * @param element     * @return     */    public boolean isContainKey(double element){        boolean flag = false;        if(element > minElement && element <= maxElement){            flag = true;        }        return flag;    }
}

首先通过一个类 ContinuousList 来存储概率集的对象，用来表示在<u>宿主轴</u>^1上。这里友情提醒一下，这里的概率集并不一定需要概率和为 100% ， 这里的概率提供方只需要提供一个权重就行了，我们在投射到<u>宿主轴</u>^1上的时候自动会一次补全的，最后也是通过随机数看在那块权重对应的索引上的。就好想将权重类似铺砖一样依次铺满就行，然后随机扔一个石子看在那一块就行。

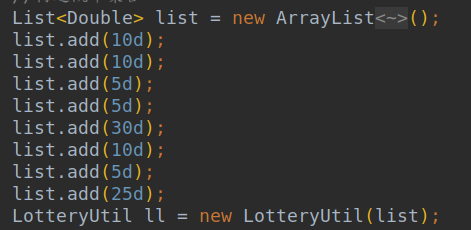
概率平铺示意图

<span id="change">改造概率集</span>

上面我们提到供应方提供的是权重，图一提供{10,10,5,5,30,10,5,25}，总和为 100(不是必须是 100，这里 100 只是为了方便观测)这些表示的意思是生成第 0 位的该路为 10/100=10%。现在加入我们有一个数组集合为{“a”,"b","c","d","e","f","g","h"}这八个字符。那么现在通过图一的构造，那么生成 a~h 的概率分别是{10%,10%,5%,5%,30%,10%,5%,25%}那么如何通过权重转变为概率的呢。

• 首先第一个元素权重为 10，则其在<u>宿主轴</u>^1上的分布范围为 0~10

• 第二个元素权重 10，对应的分布范围则为 10~20

• 第三个元素权重 5，对应的分布范围则为 20~25

• 第四个元素权重 5，对应的分布范围则为 25~30

• 第五个元素权重 30，对应的分布范围则为 30~60

• 第六个元素权重 10，对应的分布范围则为 60~70

• 第七个元素权重 5，对应的分布范围则为 70~75

• 第八个元素权重 25，对应的分布范文责问 75~100

<span id="random">随机生成概率集索引</span>

/** * 进行抽奖操作 * 返回：奖品的概率list集合中的下标 */public int randomColunmIndex(){    int index = -1;    Random r = new Random();    double d = r.nextDouble() * maxElement;  //生成0-1间的随机数    if(d == 0d){        d = r.nextDouble() * maxElement;     //防止生成0.0    }    int size = lotteryList.size();    for(int i = 0; i < size; i++){        ContinuousList cl = lotteryList.get(i);        if(cl.isContainKey(d)){            index = i;            break;        }    }    if(index == -1){        throw new IllegalArgumentException("概率集合设置不合理！");    }    return index;
}

现在我们的<u>宿主轴</u>^1已经构建好了，下面我们基于各个读者使用的语言生成 0~1 的随机数，然后按<u>宿主轴</u>^1的比例放大至<u>宿主轴</u>^1上。例如： 随机生成 0.5238 ， 上述的<u>宿主轴</u>^1长度是 100 ， 则此次生成的随机数 0.5238 对应<u>宿主轴</u>^1上的 52.38。52.38 在 30~60 这个区间范围，所以此次随机生成的所以则为 30～60 对应的索引 3(从 0 开始)

<span id="search">通过率索查找元素</span>

上面 52.38 对应的概率集合中的索引是 3，这里就解释了为什么概率集和结果集个数要对应上。因为通过<u>宿主轴</u>^1我们生成了索引，概率集和结果集个数一样就保证了我们一定会获取到结果。通过索引 3 我们获取到的结果是 d

<span id="judge">测试数据验证</span>

上面介绍了改算法的执行原理集流程，纸上得来终觉浅，现在我们将通过该算法随机生成 100000 条数据，生成的同时我们加上统计数量的算法。最后我们对比下计划生成的概率和实际生成概率就可以验证改算法了。

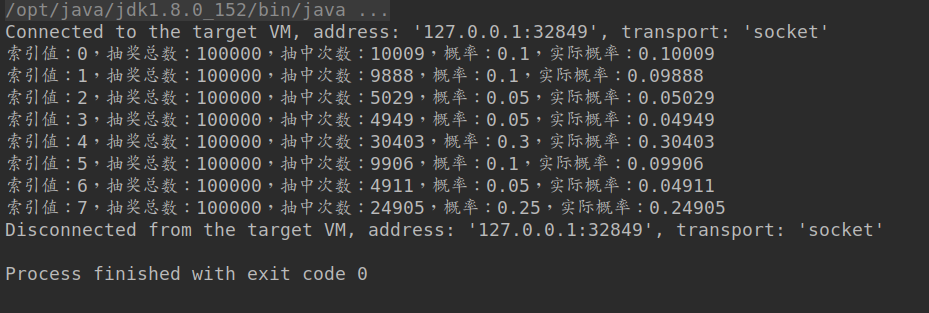
到这里也该和读者说再见了，今天的按概率生成随机数就结束了，如果读者对随机数生成原理感兴趣的话，可以对次软文拥有者建议，后续我会根据情况进行原理分析的。