K 临近算法介绍

2022 年 7 月 01 日
本文字数：2805 字
阅读完需：约 9 分钟

一、KNN 算法描述

KNN（K Near Neighbor）：找到 k 个最近的邻居，即每个样本都可以用它最接近的这 k 个邻居中所占数量最多的类别来代表。KNN 算法属于有监督学习方式的分类算法，所谓 K 近邻算法，就是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的 K 个实例（就是上面提到的 K 个邻居），如果这 K 个实例的多数属于某个类，就将该输入实例分类到这个类中。

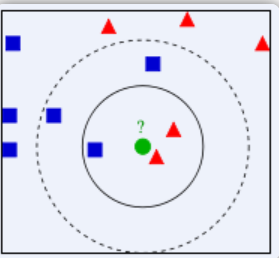
上图中有两种不同类别的样本数据，分别用蓝色正方形和红色三角形表示，最中间绿色的圆表示的数据则是待分类的数据。我们现在要解决的问题是：不知道中间的圆是属于哪一类（正方形类还是三角形类）？我们下面就来给圆分类。

从图中还能看出：如果 K=3，圆的最近的 3 个邻居是 2 个三角形和 1 个正方形，少数从属于多数，基于统计的方法，判定圆标示的这个待分类数据属于三角形一类。但是如果 K=5，圆的最近的 5 个邻居是 2 个三角形和 3 个正方形，还是少数从属于多数，判定圆标示的这个待分类数据属于正方形这一类。由此我们可以看到，当无法判定当前待分类数据从属于已知分类中的哪一类时，可以看它所处的位置特征，衡量它周围邻居的权重，而把它归为权重更大的一类，这就是 K 近邻算法分类的核心思想。

二、代码实现

算法步骤：

计算已知类别数据集中的点与当前点之间的距离；
按照距离递增依次排序；
选取与当前点距离最小的 K 个点；
确定前 k 个点所在类别的出现频率；
返回前 k 个点出现频率最高的类别作为当前点的预测分类

"""kNN: k Nearest Neighbors
Input:      inX: vector to compare to existing dataset (1xN)            dataSet: size m data set of known vectors (NxM)            labels: data set labels (1xM vector)            k: number of neighbors to use for comparison (should be an odd number)            Output:     the most popular class label"""
from numpy import *import operatorfrom os import listdir
def classify0(inX, dataSet, labels, k):    dataSetSize = dataSet.shape[0]    diffMat = tile(inX, (dataSetSize,1)) - dataSet #将inX重复成dataSetSize行1列，tile(A,n)，功能是将数组A重复n次，构成一个新的数组    sqDiffMat = diffMat**2    sqDistances = sqDiffMat.sum(axis=1) #sum(axis=1)就是将矩阵的每一行向量相加    distances = sqDistances**0.5    sortedDistIndicies = distances.argsort() #argsort()得到的是排序后数据原来位置的下标       classCount={}               for i in range(k):        voteIlabel = labels[sortedDistIndicies[i]]#确定前k个距离最小元素所在的主要分类labels        classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1        #计算各个元素标签的出现次数(频率)，当voteIlabel在classCount中时，classCount.get()返回1，否则返回0        #operator.itemgetter(1)表示按照第二个元素的次序对元组进行排序，reverse=True表示为逆序排序，即从大到小排序    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)    return sortedClassCount[0][0]   #最后返回发生频率最高的元素标签

复制代码

classify0()函数有 4 个输入参数：用于分类的输入向量是 inX，输入的训练样本集为 dataSet，标签向量为 labels，最后的参数 k 表示用于选择最近邻居的数目，其中标签向量的元素数目和矩阵 dataSet 的行数相同。除了K值之外，kNN算法的另一个核心参数是距离函数的选择。上述代码使用的是欧式距离，在日常生活中我们所说的距离往往是欧氏距离，也即平面上两点相连后线段的长度。欧氏距离的定义如下：

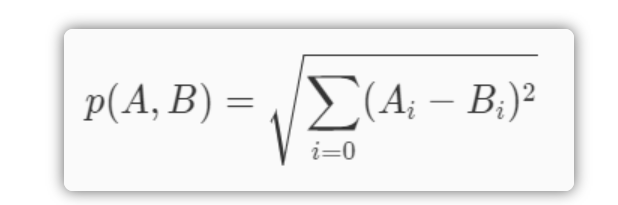
除此之外，在机器学习中常见的距离定义有以下几种：

汉明距离：两个字符串对应位置不一样的个数。汉明距离是以理查德·卫斯里·汉明的名字命名的。在信息论中，两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。换句话说，它就是将一个字符串变换成另外一个字符串所需要替换的字符个数；
马氏距离：表示数据的协方差距离。计算两个样本集相似度的距离；
余弦距离：两个向量的夹角作为一种判别距离的度量；
曼哈顿距离：两点投影到各轴上的距离总和；
切比雪夫距离：两点投影到各轴上距离的最大值；
标准化欧氏距离：欧氏距离里每一项除以标准差。

还有一种距离叫闵可夫斯基距离，如下：

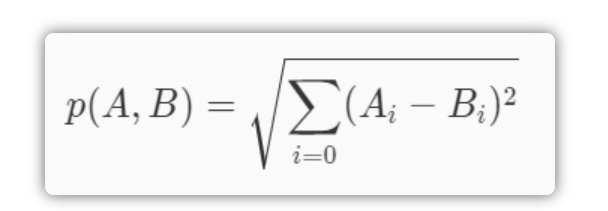
当q为1时，即为曼哈顿距离。当q为2时，即为欧氏距离。

在这里介绍距离的目的一个是为了让大家使用 k 近邻算法时，如果发现效果不太好时，可以通过使用不同的距离定义来尝试改进算法的性能。

KNN 算法的优缺点

优点：

理解简单，数学知识基本为0；
既能用于分来，又能用于回归；
支持多分类。

kNN算法可以用于回归，回归的思路是将离待测点最近的k个点的平均值作为待测点的回归预测结果。

kNN算法在测试阶段是看离待测点最近的k个点的类别比分，所以不管训练数据中有多少种类别，都可以通过类别比分来确定待测点类别。

注：当然会有类别比分打平的情况，这种情况下可以看待测点离哪个类别最近，选最近的类别作为待测点的预测类别。

缺点：

当然kNN算法的缺点也很明显，就是当训练集数据量比较大时，预测过程的效率很低。这是因为kNN算法在预测过程中需要计算待测点与训练集中所有点的距离并排序。可想而知，当数据量比较大的时候，效率会奇低。对于时间敏感的业务不太适合。

三、使用 sklearn 进行 KNN 分类与回归算法

1.使用 sklearn 中的 kNN 算法进行分类

sklearn 中 KNeighborsClassifier 的参数

代码实现：

from sklearn.neighbors import KNeighborsClassifier
def classification(train_feature, train_label, test_feature):    '''    使用KNeighborsClassifier对test_feature进行分类    :param train_feature: 训练集数据    :param train_label: 训练集标签    :param test_feature: 测试集数据    :return: 测试集预测结果    '''
    clf = KNeighborsClassifier()    clf.fit(train_feature, train_label)    predict_result = clf.predict(test_feature)    return predict_result

复制代码

2.使用 sklearn 中的 kNN 算法进行回归

当我们需要使用kNN算法进行回归器时，只需要把KNeighborsClassifier换成KNeighborsRegressor即可。KNeighborsRegressor和KNeighborsClassifier的参数是完全一样的，所以在优化模型时可以参考上述的内容。

代码实现：

from sklearn.neighbors import KNeighborsRegressor
def regression(train_feature, train_label, test_feature):    '''    使用KNeighborsRegressor对test_feature进行分类    :param train_feature: 训练集数据    :param train_label: 训练集标签    :param test_feature: 测试集数据    :return: 测试集预测结果    '''
    clf = KNeighborsRegressor()    clf.fit(train_feature, train_label)    predict_result = clf.predict(test_feature)    return predict_result

复制代码

上述为 KNN 算法的简述

发布于: 刚刚阅读数: 3

原文链接:【http://xie.infoq.cn/article/00c7becb374b8968de49ff251】。文章转载请联系作者。

乌龟哥哥

关注

正在努力寻找offer的大四小菜鸟 2021.03.16 加入

擅长 Hbuilder、VS Code、MyEclipse、AppServ、PS 等软件的安装与卸载精通 Html、CSS、JavaScript、jQuery、Java 等单词的拼写熟悉 Windows、Linux、等系统的开关机看–时间过得多快，不说了，去搬砖了

发布

暂无评论

创作场景

K 临近算法介绍

一、KNN 算法描述

二、代码实现

算法步骤：

KNN 算法的优缺点

优点：

缺点：

三、使用 sklearn 进行 KNN 分类与回归算法

1.使用 sklearn 中的 kNN 算法进行分类

sklearn 中 KNeighborsClassifier 的参数

代码实现：

2.使用 sklearn 中的 kNN 算法进行回归

代码实现：

上述为 KNN 算法的简述

乌龟哥哥

评论