再见，PCA 主成分分析！

作者：EquatorCoco

2024-06-05
福建
本文字数：1860 字
阅读完需：约 6 分钟

1. 概念：数据降维的数学方法

定义

主成分分析（PCA）是一种统计方法，通过正交变换将一组可能相关的变量转换为一组线性不相关的变量，这组新的变量称为主成分。
大白话，PCA 能够从数据中提取出最重要的特征，通过减少变量的数量来简化模型，同时保留原始数据集中的大部分信息。

特点

PCA 是最广泛使用的数据降维技术之一，能够有效地揭示数据的内部结构，减少分析问题的复杂度。

应用领域

图像处理：图像压缩和特征提取。
金融数据分析：风险管理、股票市场分析。
生物信息学：基因数据分析、疾病预测。
社会科学研究：问卷数据分析、人口研究。

2 核心原理：方差最大化

方差最大化：
PCA 通过找到数据方差最大的方向来确定主成分，然后找到次大方向，且这些方向必须是相互正交的。
这样做的目的是保证降维后的数据能够保留最多的原始数据信息。

计算步骤：

数据标准化：使得每个特征的平均值为 0，方差为 1。
计算协方差矩阵：反映变量之间的相关性。
计算协方差矩阵的特征值和特征向量：特征向量决定了 PCA 的方向，特征值决定了方向的重要性。
选择主成分：根据特征值的大小，选择最重要的几个特征向量，构成新的特征空间。

3 优缺点分析

优点：

降维效果显著：能够有效地减少数据的维度，同时尽可能地保留原始数据的信息。
揭示数据结构：有助于发现数据中的模式和结构，便于进一步分析。
无需标签数据：PCA 是一种无监督学习算法，不需要数据标签。

缺点：

线性限制：PCA 只能捕捉到数据的线性关系和结构，对于非线性结构无能为力。
方差并非信息量的唯一衡量：有时候数据的重要性并不仅仅体现在方差上，PCA 可能会忽略掉一些重要信息。
对异常值敏感：异常值可能会对 PCA 的结果产生较大影响。

4 PCA 实战

介绍一个用于主成分分析的 Python 库

PCA 的核心是构建在 sklearn 功能之上，以便在与其他包结合时实现最大的兼容性。

除了常规的 PCA 外，它还可以执行 SparsePCA 和 TruncatedSVD。

其他功能包括：

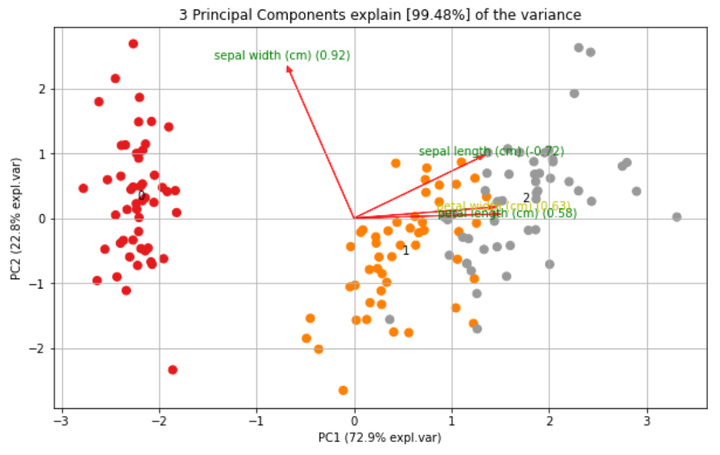
使用 Biplot 绘制载荷图
确定解释的方差
提取性能最佳的特征
使用载荷绘制的散点图
使用 Hotelling T2 和/或 SPE/Dmodx 进行异常值检测

pip install pca

复制代码


from pca import pca  # 导入PCA模块import numpy as npimport pandas as pd
# Datasetfrom sklearn.datasets import load_iris  # 导入鸢尾花数据集
# 从鸢尾花数据集中创建DataFrame对象X = pd.DataFrame(data=load_iris().data, columns=load_iris().feature_names, index=load_iris().target)
# 初始化PCA模型，指定主成分数量为3，并进行数据标准化model = pca(n_components=3, normalize=True)
# 拟合并转换数据out = model.fit_transform(X)
# 创建只包含方向的图fig, ax = model.biplot(textlabel=True, legend=False, figsize=(10, 6))

复制代码

下面我们使用 sklearn 里面的 PCA 工具，在一组人脸数据上直观感受下，


# 导入必要的库import numpy as npimport matplotlib.pyplot as pltfrom sklearn.datasets import fetch_olivetti_facesfrom sklearn.decomposition import PCA
# 加载Olivetti人脸数据集faces_data = fetch_olivetti_faces()X = faces_data.data
# 可视化原始图像和对应的主成分n_images = 4  # 每行显示的图像数量n_rows = 4    # 总共的行数
fig, axes = plt.subplots(n_rows, 2*n_images, figsize=(16, 10), subplot_kw={'xticks':[], 'yticks':[]})
# 使用PCA降维n_components = 50  # 设置PCA保留的主成分数量pca = PCA(n_components=n_components, whiten=True, random_state=42)X_pca = pca.fit_transform(X)
for r in range(n_rows):    for i in range(n_images):        index = r * n_images + i                axes[r, 2*i].imshow(X[index].reshape(64, 64), cmap='gray')        axes[r, 2*i].set_title(f'大侠 {index+1} 图像', fontproperties='SimHei')  # 手动设置字体
        axes[r, 2*i+1].imshow(pca.inverse_transform(X_pca[index]).reshape(64, 64), cmap='bone')        axes[r, 2*i+1].set_title(f'大侠 {index+1} 主成分', fontproperties='SimHei')  # 手动设置字体
plt.tight_layout()plt.show()

复制代码

我们保留了前 50 个主成分

通过可视化对比图直观感受下，信息保留了多多少，损失了多少

通过对比图可以看到，某一张人脸的基本信息都保留了下来

如果保留前 100 个主成分，那就更接近原始图片了

你也可以试下，保留 1 个主成分会怎样？通过保留的信息你还认得出来哪过大侠是哪过吗

文章转载自：算法金「全网同名」
原文链接：https://www.cnblogs.com/suanfajin/p/18230769
体验地址：http://www.jnpfsoft.com/?from=infoq

发布于: 刚刚阅读数: 2

EquatorCoco

关注

还未添加个人签名 2023-06-19 加入

还未添加个人简介

发布

暂无评论

创作场景

再见，PCA 主成分分析！

1. 概念：数据降维的数学方法

2 核心原理：方差最大化

3 优缺点分析

4 PCA 实战

EquatorCoco

评论