主成分分析 PCA 与奇异值分解 SVD-PCA 中的 SVD

svd_solver 是奇异值分解器的意思，为什么 PCA 算法下面会有有关奇异值分解的参数？不是两种算法么？

PCA：方阵的特征值分解，对于一个方阵$A$，总可以写成：

$$A=Q\Lambda Q^{-1}$$

其中，Q 是这个矩阵 A 的特征向量组成的矩阵，$\Lambda$是一个对角矩阵，每一个对角线元素就是一个特征值，里面的特征值是由小排列的，这些特征值所对应的特征向量就是描述这个矩阵变化方向（从主要的变化到次要的变化排列）。也就是说矩阵 A 的信息可以由其特征值和特征向量表示。SVD：矩阵的奇异值分解其实就是对于矩阵 A 的协方差矩阵$A^{T}A$和$A{A}^T$做特征值分解推导出来的：

$$A_{m,n}=U_{m,m}{\Lambda }_{m,n}{V}_{n,n}^T\approx U_{m,k}{\Lambda }_{k,k}{V}_{n,k}^T$$

其中：$U,V$都是正交矩阵，有$U^{T}U=I_m,V^{T}V=I_n$。这里的约等于是因为$\Lambda$中有 n 个奇异值，但是由于排在后面的很多接近 0，所以我们可以仅保留比较大的 k 个奇异值。

注意这并不是把数据降到 k 维，如果要降维，应该是改变的是$V_{n,k}^T$中 n 的数值

实际上 Sklearn 的 PCA 就是用 SVD 进行求解的，原因有以下几点：

1. 当样本维度很高时，协方差矩阵计算太慢；

2. 方阵特征值分解计算效率不高；

3. SVD 除了特征值分解这种求解方式外，还有更高效更准球的迭代求解方式，避免了$A^{T}A$的计算；

4. 其实 PCA 的效果与 SVD 的右奇异向量的压缩效果相同。

作者：阿泽链接：【机器学习】降维——PCA（非常详细） - 知乎 (zhihu.com)

这里我们令 k 就是n_components的取值，是我们降维后希望得到的维度。若 X 为(m,n)的特征矩阵， 就是结构为(n,n)的矩阵，取这个矩阵的前 k 行（进行切片），即将 V 转换为结构为(k,n)的矩阵。而**$V_{(k,n)}^T$与原特征矩阵 X 相乘，即可得到降维后的特征矩阵$X_{dr}$。这是说**，奇异值分解可以不计算协方差矩阵等等结构复杂计算冗长的矩阵，就直接求出新特征空间和降维后的特征矩阵。

左奇异矩阵可以用于行数的压缩。右奇异矩阵可以用于列数即特征维度的压缩，也就是我们的 PCA 降维。

作者：失而复得的时间链接：notes for PCA - 知乎 (zhihu.com)

这里主要说明一下右奇异矩阵的作用

假设我们矩阵每一行表示一个样本，每一列表示一个 feature，用矩阵的语言来表示，将一个$m\times n$的矩阵 A 的进行坐标轴的变化，P 就是一个变换的矩阵从一个 N 维的空间变换到另一个 N 维的空间，在空间中就会进行一些类似于旋转、拉伸的变化。

$$A_{m,n}{P}_{m,n}=\widetilde{A_{m,n}}$$

而将一个$m\times n$的矩阵 A 变换成一个$m\times r$的矩阵，这样就会使得本来有 n 个 feature 的，变成了有 r 个 feature 了（r < n)，这 r 个其实就是对 n 个 feature 的一种提炼，我们就把这个称为 feature 的压缩。用数学语言表示就是：

$$A_{m,n}{P}_{n,r}=\widetilde{A_{m,r}}$$

但是这个怎么和 SVD 扯上关系呢？之前谈到，SVD 得出的奇异向量也是从奇异值由大到小排列的，按 PCA 的观点来看，就是方差最大的坐标轴就是第一个奇异向量，方差次大的坐标轴就是第二个奇异向量…我们回忆一下之前得到的 SVD 式子：

$$A_{m,n}\approx U_{m,r}{\Sigma }_{r,r}{V}_{r,n}^T$$

这里约等于是因为我们对 A 进行了降维的操作，实际上想要得到的是$\widetilde{A_{m,r}}$

在矩阵的两边同时乘上一个矩阵 V，由于 V 是一个正交的矩阵，所以 V 转置乘以 V 得到单位阵$\text{I}$，所以可以化成后面的式子

$$A_{m,n}{V}_{r,n}=U_{m,r}{\Sigma }_{r,r}$$

将后面的式子与$A\cdot P$那个$m\times n$的矩阵变换为$m\times r$的矩阵的式子对照看看，在这里，其实 V 就是 P，也就是一个变化的向量。这里是将一个$m\times n$的矩阵压缩到一个$m\times r$的矩阵，也就是对列进行压缩

作者：LeftNotEasy - 博客园 (cnblogs.com)链接：机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用 - LeftNotEasy - 博客园 (cnblogs.com)

简而言之，SVD 在矩阵分解中的过程比 PCA 简单快速，虽然两个算法都走一样的分解流程，但 SVD 可以直接算出 V。但是遗憾的是，SVD 的信息量衡量指标比较复杂，要理解”奇异值“远不如理解”方差“来得容易，因此， sklearn 将降维流程拆成了两部分：一部分是计算特征空间 V，由奇异值分解完成，另一部分是映射数据和求解新特征矩阵，由主成分分析完成，实现了用 SVD 的性质减少计算量，却让信息量的评估指标是方差，具体流程如下图：

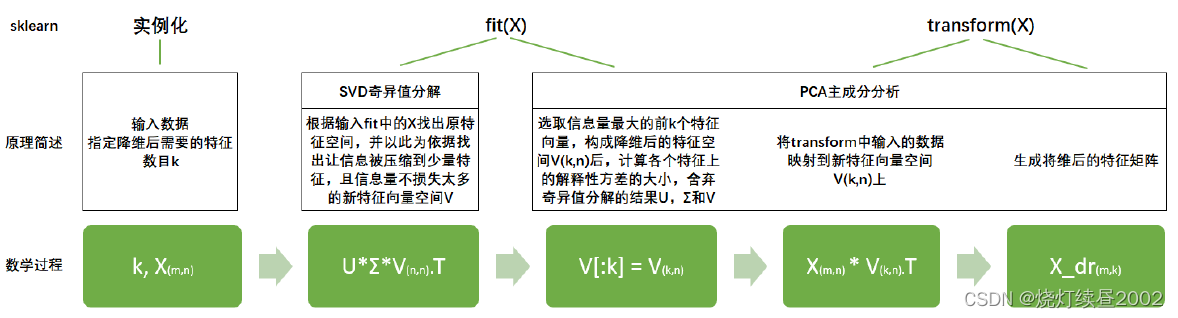
讲到这里，相信大家就能够理解，为什么 PCA 的类里会包含控制 SVD 分解器的参数了。通过 SVD 和 PCA 的合作， sklearn 实现了一种计算更快更简单，但效果却很好的“合作降维“。很多人理解 SVD，是把 SVD 当作 PCA 的一种求解方法，其实指的就是在矩阵分解时不使用 PCA 本身的特征值分解，而使用奇异值分解来减少计算量。这种方法确实存在，但在 sklearn 中，矩阵 U 和$\Sigma$虽然会被计算出来（同样也是一种比起 PCA 来说简化非常多的数学过程，不产生协方差矩阵），但完全不会被用到，也无法调取查看或者使用，因此我们可以认为，U 和$\Sigma$在fit 过后就被遗弃了。奇异值分解追求的仅仅是 V，只要有了 V，就可以计算出降维后的特征矩阵。在 transform 过程之后，fit 中奇异值分解的结果除了 V(k,n)以外，就会被舍弃，而 V(k,n)会被保存在属性 components_ 当中，可以调用查看。

PCA(2).fit(X).components_---array([[ 0.36138659, -0.08452251,  0.85667061,  0.3582892 ],       [ 0.65658877,  0.73016143, -0.17337266, -0.07548102]])
PCA(2).fit(X).components_.shape---(2, 4)

在这里需要注意的是 sklearn 并非对原数据矩阵进行 SVD，而是对中心化的 X 进行 SVD，中心化也就是每个特征减去所有样本该特征的均值

from sklearn.decomposition import PCA
import pandas as pd
import numpy as np

data = pd.DataFrame(np.random.randint(0,10,[4,5]))
data
---
    0  1  2  3  4
0  1  2  9  8  9
1  0  0  9  7  2
2  5  8  0  4  6
3  8  1  7  4  3

pca = PCA(svd_solver='full').fit(data)
data_n = pca.transform(data)
data_n
---
array([[-3.56575962e+00, -4.20351474e+00, -2.24795956e+00,
      4.44089210e-16],
    [-5.32376396e+00,  7.19100316e-01,  3.01296068e+00,
     -1.27675648e-15],
    [ 8.29225332e+00, -1.72080169e+00,  1.10221431e+00,
      1.88737914e-15],
    [ 5.97270255e-01,  5.20521611e+00, -1.86721544e+00,
     -1.22124533e-15]])

data_m = data - data.mean()
# 对于一个DataFrame对象，.mean()表示要每一列的均值
# 对于一个ndarry对象，.mean()表示所有数值的均值
data_m # 中心化
---
    0  1  2  3  4
0  -2.5  -0.75  2.75  2.25  4.0
1  -3.5  -2.75  2.75  1.25  -3.0
2  1.5  5.25  -6.25  -1.75  1.0
3  4.5  -1.75  0.75  -1.75  -2.0

np.dot(data_m,np.linalg.pinv(pca.components_)) # 套件实现V^T的伪逆矩阵
np.dot(data_m, np.dot(pca.components_.T,np.linalg.inv(np.dot(pca.components_,pca.components_.T)))) # 手动实现V^T的伪逆矩阵
# 对于一个矩阵V，其伪逆矩阵为V(V^T V)^-1
np.dot(data_m,pca.components_.T) # V^T的转置
# 结果都和data_n一样
# 这里也能说明V和V^T的伪逆矩阵相同

视频作者：菜菜TsaiTsai链接：【技术干货】菜菜的机器学习sklearn【全85集】Python进阶_哔哩哔哩_bilibili