神经网络是深度学习的基础，正是深度学习的兴起，让停滞不前的人工智能再一次的取得飞速的发展。

其实神经网络的理论由来已久，灵感来自仿生智能计算，只是以前限于硬件的计算能力，没有突出的表现，直至谷歌的 AlphaGO 的出现，才让大家再次看到神经网络相较于传统机器学习的优异表现。

本文主要介绍神经网络中的重要基础概念，然后基于这些概念手工实现一个简单的神经网络。希望通过理论结合实践的方式让大家更容易的理解神经网络。

1. 神经网络是什么

神经网络就像人脑一样，整体看上去非常复杂，但是其基础组成部分并不复杂。其组成部分中最重要的就是神经元（neural），sigmod 函数和层（layer）。

1.1. 神经元

神经元（neural）是神经网络最基本的元素，一个神经元包含 3 个部分：

• 获取输入：获取多个输入的数据

• 数学处理：对输入的数据进行数学计算

• 产生输出：计算后多个输入数据变成一个输出数据

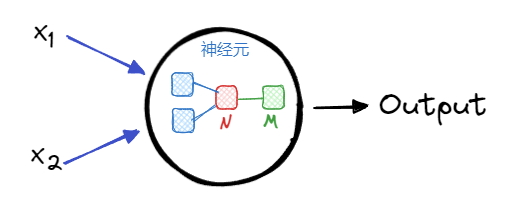
从上图中可以看出，神经元中的处理有 2 个步骤。第一个步骤：从蓝色框变成红色框，是对输入的数据进行加权计算后合并为一个值（N）。N=x1w1+x2w2𝑁=𝑥1𝑤1+𝑥2𝑤2 其中，w1,w2𝑤1,𝑤2 分别是输入数据 x1,x2𝑥1,𝑥2 的权重。一般在计算 N𝑁的过程中，除了权重，还会加上一个偏移参数 b𝑏，最终得到：N=x1w1+x2w2+b𝑁=𝑥1𝑤1+𝑥2𝑤2+𝑏

第二个步骤：从红色框变成绿色框，通过 sigmoid 函数是对N进一步加工得到的神经元的最终输出（M）。

1.2. sigmoid 函数

sigmoid函数也被称为 S 函数，因为的形状类似 S 形。

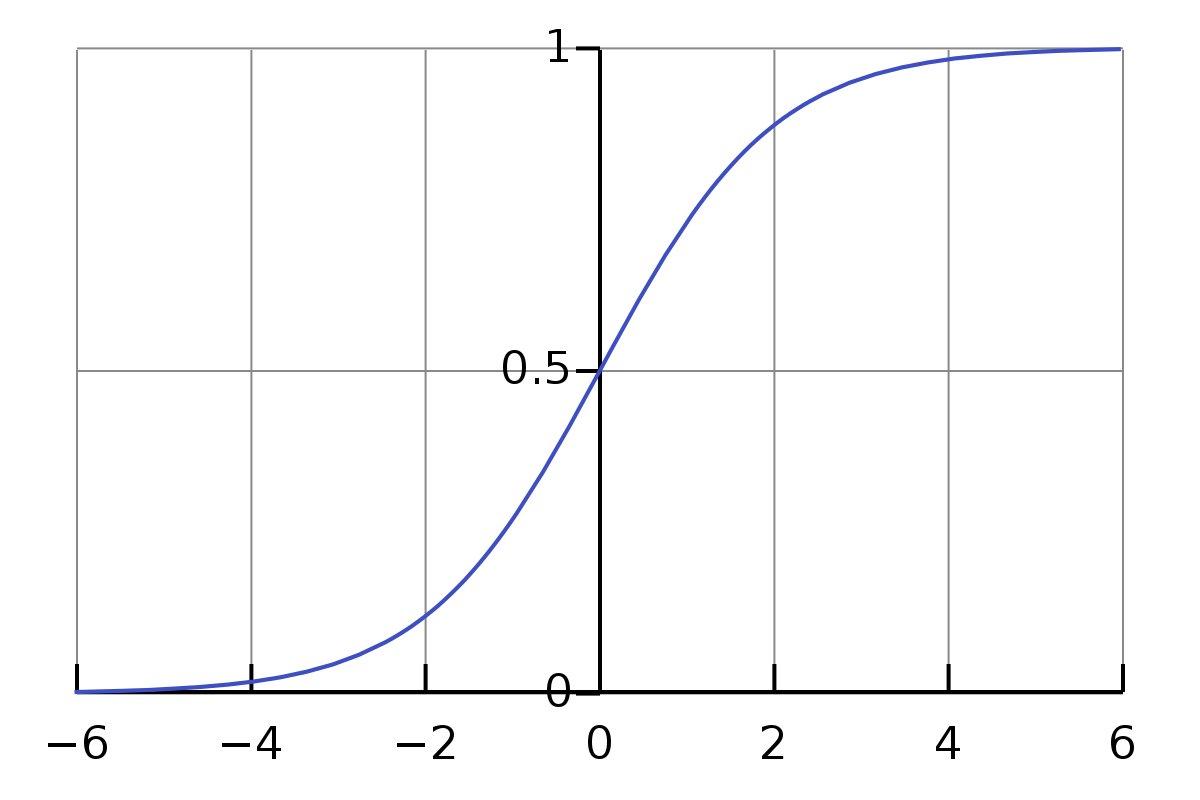
它是神经元中的重要函数，能够将输入数据的值映射到(0,1)(0,1)之间。最常用的sigmoid函数是 f(x)=11+e−x𝑓(𝑥)=11+𝑒−𝑥，当然，不是只有这一种sigmoid函数。

至此，神经元通过两个步骤，就把输入的多个数据，转换为一个(0,1)(0,1)之间的值。

1.3. 层

多个神经元可以组合成一层，一个神经网络一般包含一个输入层和一个输出层，以及多个隐藏层。

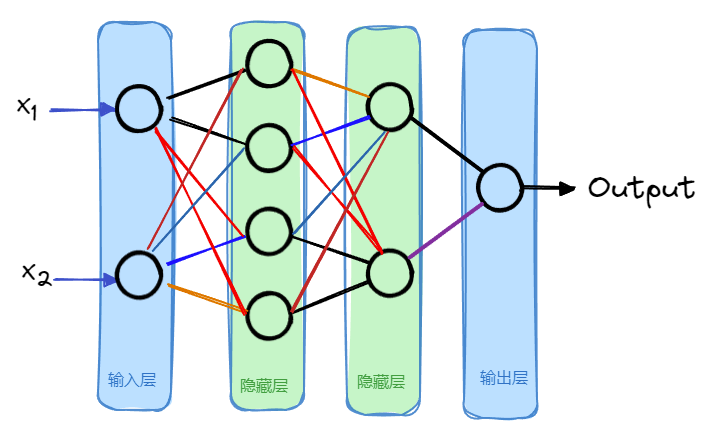
比如上图中，有 2 个隐藏层，每个隐藏层中分别有 4 个和 2 个神经元。实际的神经网络中，隐藏层数量和其中的神经元数量都是不固定的，根据模型实际的效果来进行调整。

1.4. 网络

通过神经元和层的组合就构成了一个网络，神经网络的名称由此而来。神经网络可大可小，可简单可复杂，不过，太过简单的神经网络模型效果一般不会太好。

因为一只果蝇就有 10 万个神经元，而人类的大脑则有大约 1000 亿个神经元，这就是为什么训练一个可用的神经网络模型需要庞大的算力，这也是为什么神经网络的理论 1943 年就提出了，但是基于深度学习的AlphaGO却诞生于 2015 年。

2. 实现一个神经网络

了解上面的基本概念只能形成一个感性的认知。下面通过自己动手实现一个最简单的神经网络，来进一步认识神经元，sigmoid 函数以及隐藏层是如何发挥作用的。

2.1. 准备数据

数据使用sklearn库中经典的鸢尾花数据集，这个数据集中有 3 个分类的鸢尾花，每个分类 50 条数据。为了简化，只取其中前100条数据来使用，也就是取 2 个分类的鸢尾花数据。

from sklearn.datasets import load_iris
ds = load_iris(as_frame=True, return_X_y=True)data = ds[0].iloc[:100]target = ds[1][:100]
print(data)print(target)

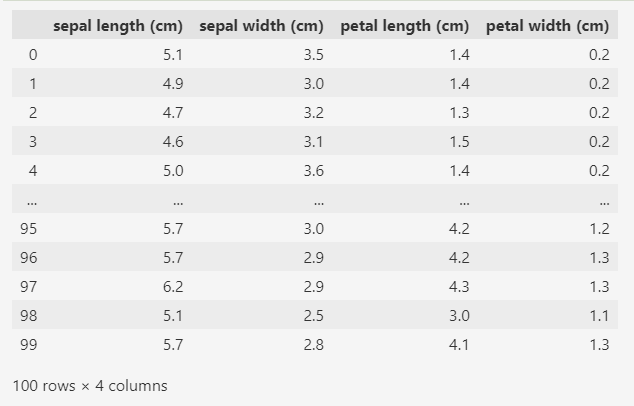
变量data中100条数据，每条数据包含 4 个属性，分别是花萼的宽度和长度，花瓣的宽度和长度。

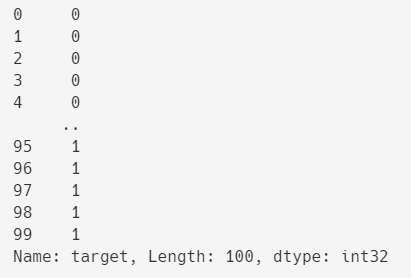
变量target中也是100条数据，只有 0 和 1 两种值，表示两种不同种类的鸢尾花。

2.2. 实现神经元

准备好了数据，下面开始逐步实现一个简单的神经网络。首先，实现最基本的单元--神经元。本文第一节中已经介绍了神经元中主要的 2 个步骤，分别计算出 N𝑁和 M𝑀。

计算 N𝑁时，依据每个输入元素的权重（w1,w2𝑤1,𝑤2）和整体的偏移 b𝑏；计算 M𝑀时，通过sigmoid函数。

def sigmoid(x):    return 1 / (1 + np.exp(-1 * x))
@dataclassclass Neuron:    weights: list[float] = field(default_factory=lambda: [])    bias: float = 0.0    N: float = 0.0    M: float = 0.0
    def compute(self, inputs):        self.N = np.dot(self.weights, inputs) + self.bias        self.M = sigmoid(self.N)        return self.M

上面的代码中，Neuron类表示神经元，这个类有 4 个属性：其中属性weights和bias是计算 N𝑁时的权重和偏移；属性N和M分别是神经元中两步计算的结果。

Neuron类的compute方法根据输入的数据计算神经元的输出。

2.3. 实现神经网络

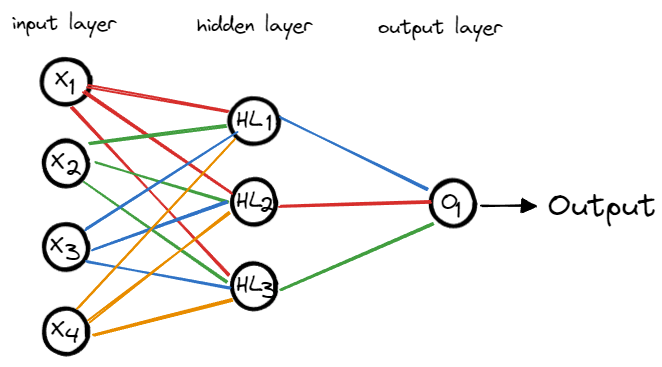
神经元实现之后，下面就是构建神经网络。我们的输入数据是带有 4 个属性（花萼的宽度和长度，花瓣的宽度和长度）的鸢尾花数据，所以神经网络的输入层有 4 个值（x1,x2,x3,x4𝑥1,𝑥2,𝑥3,𝑥4）。

为了简单起见，我们的神经网络只构建一个隐藏层，其中包含 3 个神经元。最后就是输出层，输出层最后输出一个值，表示鸢尾花的种类。

由此形成的简单神经网络如下图所示：

实现的代码：

@dataclassclass MyNeuronNetwork:    HL1: Neuron = field(init=False)    HL2: Neuron = field(init=False)    HL3: Neuron = field(init=False)    O1: Neuron = field(init=False)
    def __post_init__(self):        self.HL1 = Neuron()        self.HL1.weights = np.random.dirichlet(np.ones(4))        self.HL1.bias = np.random.normal()
        self.HL2 = Neuron()        self.HL2.weights = np.random.dirichlet(np.ones(4))        self.HL2.bias = np.random.normal()
        self.HL3 = Neuron()        self.HL3.weights = np.random.dirichlet(np.ones(4))        self.HL3.bias = np.random.normal()
        self.O1 = Neuron()        self.O1.weights = np.random.dirichlet(np.ones(3))        self.O1.bias = np.random.normal()
    def compute(self, inputs):        m1 = self.HL1.compute(inputs)        m2 = self.HL2.compute(inputs)        m3 = self.HL3.compute(inputs)
        output = self.O1.compute([m1, m2, m3])        return output

MyNeuronNetwork类是自定义的神经网络，其中的属性是 4 个神经元。HL1，HL2，HL3是隐藏层的 3 个神经元；O1是输出层的神经元。

__post__init__函数是为了初始化各个神经元。因为输入层是 4 个属性（x1,x2,x3,x4𝑥1,𝑥2,𝑥3,𝑥4），所以神经元HL1，HL2，HL3的weights初始化为 4 个随机数组成的列表，偏移（bias）用一个随时数来初始化。

对于神经元O1，它的输入是隐藏层的 3 个神经元，所以它的weights初始化为 3 个随机数组成的列表，偏移（bias）还是用一个随时数来初始化。

最后还有一个compute函数，这个函数描述的就是整个神经网络的计算过程。首先，根据输入层（x1,x2,x3,x4𝑥1,𝑥2,𝑥3,𝑥4）的数据计算隐藏层的神经元（HL1，HL2，HL3）；然后，以隐藏层的神经元（HL1，HL2，HL3）的输出作为输出层的神经元（O1）的输入，并将O1的计算结果作为整个神经网络的输出。

2.4. 训练模型

上面的神经网络中各个神经元的中的参数（主要是weights和bias）都是随机生成的，所以直接使用这个神经网络，效果一定不会很好。所以，我们需要给神经网络（MyNeuronNetwork类）加一个训练函数，用来训练神经网络中各个神经元的参数（也就是个各个神经元中的weights和bias）。

@dataclassclass MyNeuronNetwork:    # 略...
    def train(self, data: pd.DataFrame, target: pd.Series):        ## 使用 随机梯度下降算法来训练        pass

上面的train函数有两个参数data（训练数据）和target（训练数据的标签）。我们使用随机梯度下降算法来训练模型的参数。这里略去了具体的代码，完整的代码可以在文章的末尾下载。

此外，再实现一个预测函数predict，传入测试数据集，然后用我们训练好的神经网络模型来预测测试数据集的标签。

@dataclassclass MyNeuronNetwork:    # 略...        def predict(self, data: pd.DataFrame):
        results = []        for idx, row in enumerate(data.values):            pred = self.compute(row)            results.append(round(pred))
        return results

2.5. 验证模型效果

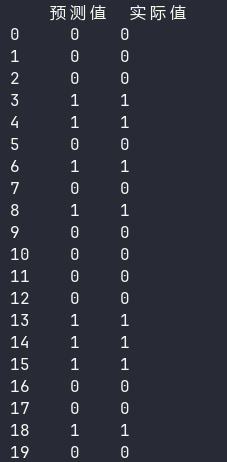
最后就是验证模型的效果。

def main():    # 加载数据    ds = load_iris(as_frame=True, return_X_y=True)
    # 只用前100条数据    data = ds[0].iloc[:100]    target = ds[1][:100]
    # 划分训练数据，测试数据    # test_size=0.2 表示80%作为训练数据，20%作为测试数据    X_train, X_test, y_train, y_test = train_test_split(data, target, test_size=0.2)
    # 创建神经网络    nn = MyNeuronNetwork()
    # 用训练数据集来训练模型    nn.train(X_train, y_train)
    # 检验模型    # 用训练过的模型来预测测试数据的标签    results = nn.predict(X_test)    df = pd.DataFrame()    df["预测值"] = results    df["实际值"] = y_test.values    print(df)

运行结果可以看出，模型的效果还不错，20 条测试数据的预测结果都正确。

3. 总结

本文中的的神经网络示例是为了介绍神经网络的一些基本概念，所以对神经网络做了尽可能的简化，为了方便去手工实现。

而实际环境中的神经网络，不仅神经元的个数，隐藏层的数量极其庞大，而且其计算和训练的方式也很复杂，手工去实现不太可能，一般会借助TensorFlow，Keras和PyTorch等等知名的 python 深度学习库来帮助我们实现。

文章转载自：wang_yb

原文链接：https://www.cnblogs.com/wang_yb/p/18176563

体验地址：http://www.jnpfsoft.com/?from=infoq