一、线性回归
背景:
线性回归是最古老也是最简单的回归算法之一,其历史可以追溯到 18 世纪,这种方法在统计学中占据了重要地位,成为许多复杂算法的基础。
原理:
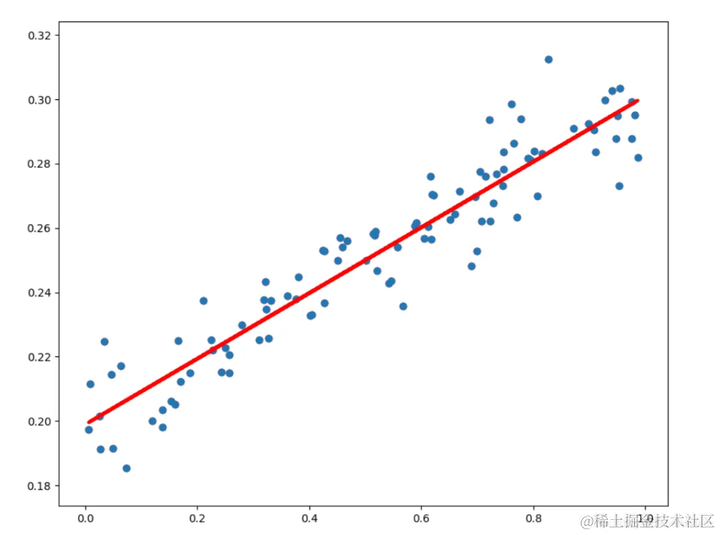
线性回归通过寻找数据点之间的最佳拟合直线,来预测目标变量。其数学模型为:
其中,( y ) 是目标变量,( x ) 是特征变量,( \beta_0 ) 和 ( \beta_1 ) 分别为截距和斜率,( \epsilon ) 是误差项。我们通过最小化均方误差(Mean Squared Error, MSE)来估计这些参数:
优缺点:
优点:
缺点:
线性假设:假设特征和目标变量之间是线性关系,无法捕捉非线性关系。
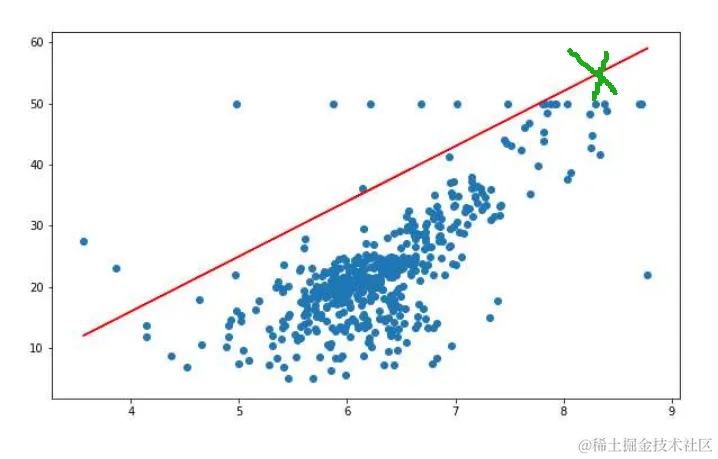
对异常值敏感:异常值(outliers)会显著影响模型参数的估计。
多重共线性:特征之间的多重共线性会导致参数估计不稳定。
(图:对异常值敏感)
应用场景:
线性回归在经济学、金融学、社会学等领域有广泛应用。以下是一些具体的应用场景:
经济学:线性回归用于预测消费支出和收入之间的关系。例如,经济学家可以通过分析历史数据,建立模型来预测未来的消费趋势。
金融学:线性回归用于股票价格预测和风险管理。例如,金融分析师可以使用历史股票价格数据,建立模型来预测未来的价格走势。
社会学:线性回归用于研究社会现象之间的关系。例如,社会学家可以分析教育水平和收入之间的关系,发现教育对收入的影响。
实际案例和代码示例
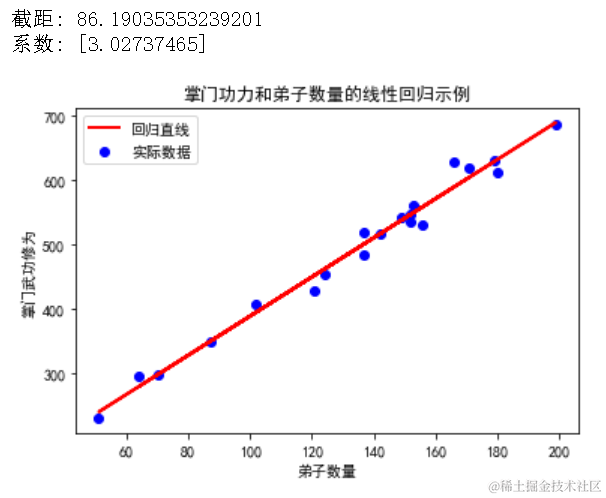
假设我们有一组数据,记录了某武侠小说中不同门派的弟子数和他们掌门的武功修为。我们可以使用线性回归来预测弟子数对掌门武功修为的影响。
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.linear_model import LinearRegression
# 生成模拟数据np.random.seed(42)disciple_count = np.random.randint(50, 200, size=20)master_skill = 3 * disciple_count + np.random.randn(20) * 20 + 100
# 数据转换为二维数组X = disciple_count.reshape(-1, 1)y = master_skill
# 创建线性回归模型并训练lin_reg = LinearRegression()lin_reg.fit(X, y)
# 打印模型参数print("截距:", lin_reg.intercept_)print("系数:", lin_reg.coef_)
# 可视化回归直线plt.scatter(X, y, color='blue', label='实际数据')plt.plot(X, lin_reg.predict(X), color='red', linewidth=2, label='回归直线')plt.title("掌门功力和弟子数量的线性回归示例")plt.xlabel("弟子数量")plt.ylabel("掌门武功修为")plt.legend()
复制代码
二、多元线性回归
定义和背景
多元线性回归是线性回归的扩展,适用于多个自变量预测一个因变量的情况。它通过寻找多个自变量与因变量之间的最佳拟合平面来进行预测。多元线性回归可以帮助我们理解多个因素对结果的综合影响。
适用场景和优点
多元线性回归适用于分析多个因素对结果的影响,例如分析房价与房屋面积、位置、房龄等多个因素之间的关系。其主要优点包括能够处理多个变量、提供更详细的分析和预测、更适合复杂的实际应用场景。
实际案例和代码示例
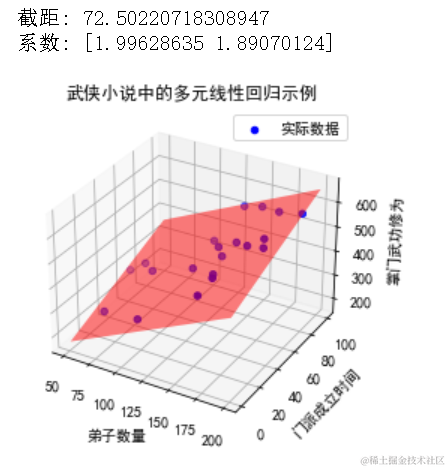
假设我们有一组数据,记录了某武侠小说中不同门派的弟子数量、门派成立时间、以及掌门的武功修为。我们可以使用多元线性回归来预测这些因素对掌门武功修为的影响。
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.linear_model import LinearRegressionfrom mpl_toolkits.mplot3d import Axes3D
# 生成模拟数据np.random.seed(42)disciple_count = np.random.randint(50, 200, size=20)establishment_years = np.random.randint(1, 100, size=20)master_skill = 2 * disciple_count + 1.5 * establishment_years + np.random.randn(20) * 20 + 100
# 数据转换为二维数组X = np.column_stack((disciple_count, establishment_years))y = master_skill
# 创建多元线性回归模型并训练lin_reg = LinearRegression()lin_reg.fit(X, y)
# 打印模型参数print("截距:", lin_reg.intercept_)print("系数:", lin_reg.coef_)
# 可视化回归平面fig = plt.figure()ax = fig.add_subplot(111, projection='3d')ax.scatter(disciple_count, establishment_years, master_skill, color='blue', label='实际数据')
# 创建用于绘制回归平面的网格xx, yy = np.meshgrid(np.linspace(50, 200, 10), np.linspace(1, 100, 10))zz = lin_reg.intercept_ + lin_reg.coef_[0] * xx + lin_reg.coef_[1] * yyax.plot_surface(xx, yy, zz, color='red', alpha=0.5, rstride=100, cstride=100)
ax.set_title("武侠小说中的多元线性回归示例")ax.set_xlabel("弟子数量")ax.set_ylabel("门派成立时间")ax.set_zlabel("掌门武功修为")ax.legend()plt.show()
复制代码
三、岭回归
定义和背景
岭回归(Ridge Regression)是一种改进的线性回归方法,主要用于处理多重共线性的问题。它通过在损失函数中加入一个惩罚项,使得回归系数尽量小,以此来减少模型的复杂度和过拟合风险。
适用场景和优点
岭回归适用于存在多重共线性的问题,尤其是当自变量之间存在较强相关性时。其主要优点包括:通过惩罚项减少过拟合、提高模型的稳定性和鲁棒性、适合处理高维数据。
实际案例和代码示例
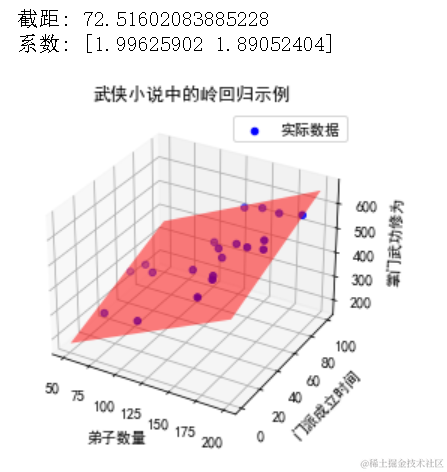
假设我们有一组数据,记录了某武侠小说中不同门派的弟子数量、门派成立时间以及掌门的武功修为。我们可以使用岭回归来预测这些因素对掌门武功修为的影响。
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.linear_model import Ridge
# 生成模拟数据np.random.seed(42)disciple_count = np.random.randint(50, 200, size=20)establishment_years = np.random.randint(1, 100, size=20)master_skill = 2 * disciple_count + 1.5 * establishment_years + np.random.randn(20) * 20 + 100
# 数据转换为二维数组X = np.column_stack((disciple_count, establishment_years))y = master_skill
# 创建岭回归模型并训练ridge_reg = Ridge(alpha=1.0)ridge_reg.fit(X, y)
# 打印模型参数print("截距:", ridge_reg.intercept_)print("系数:", ridge_reg.coef_)
# 可视化回归平面fig = plt.figure()ax = fig.add_subplot(111, projection='3d')ax.scatter(disciple_count, establishment_years, master_skill, color='blue', label='实际数据')
# 创建用于绘制回归平面的网格xx, yy = np.meshgrid(np.linspace(50, 200, 10), np.linspace(1, 100, 10))zz = ridge_reg.intercept_ + ridge_reg.coef_[0] * xx + ridge_reg.coef_[1] * yyax.plot_surface(xx, yy, zz, color='red', alpha=0.5, rstride=100, cstride=100)
ax.set_title("武侠小说中的岭回归示例")ax.set_xlabel("弟子数量")ax.set_ylabel("门派成立时间")ax.set_zlabel("掌门武功修为")ax.legend()plt.show()
复制代码
四、Lasso 回归
定义和背景
Lasso 回归(Least Absolute Shrinkage and Selection Operator)是一种改进的线性回归方法,通过引入 L1 正则化项来进行特征选择和缩减。与岭回归不同,Lasso 回归不仅能缩小回归系数,还能将一些回归系数缩减为零,从而实现特征选择。
适用场景和优点
Lasso 回归适用于需要进行特征选择的情况,特别是在高维数据中效果显著。其主要优点包括:通过特征选择提高模型的解释性、减少模型的复杂度和过拟合、适合处理高维数据。
实际案例和代码示例
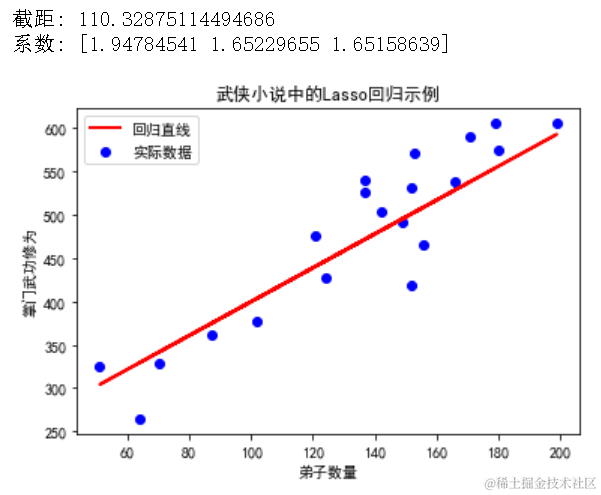
假设我们有一组数据,记录了某武侠小说中不同门派的弟子数量、门派成立时间、武器种类数量以及掌门的武功修为。我们可以使用 Lasso 回归来预测这些因素对掌门武功修为的影响。
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.linear_model import Lasso
# 生成模拟数据np.random.seed(42)disciple_count = np.random.randint(50, 200, size=20)establishment_years = np.random.randint(1, 100, size=20)weapon_types = np.random.randint(1, 10, size=20)master_skill = 2 * disciple_count + 1.5 * establishment_years + 3 * weapon_types + np.random.randn(20) * 20 + 100
# 数据转换为二维数组X = np.column_stack((disciple_count, establishment_years, weapon_types))y = master_skill
# 创建Lasso回归模型并训练lasso_reg = Lasso(alpha=0.1)lasso_reg.fit(X, y)
# 打印模型参数print("截距:", lasso_reg.intercept_)print("系数:", lasso_reg.coef_)
# 可视化回归平面(这里只能展示两个特征的二维平面图)plt.scatter(disciple_count, master_skill, color='blue', label='实际数据')plt.plot(disciple_count, lasso_reg.intercept_ + lasso_reg.coef_[0] * disciple_count + lasso_reg.coef_[1] * np.mean(establishment_years), color='red', linewidth=2, label='回归直线')plt.title("武侠小说中的Lasso回归示例")plt.xlabel("弟子数量")plt.ylabel("掌门武功修为")plt.legend()plt.show()
复制代码
五、决策树回归
定义和背景
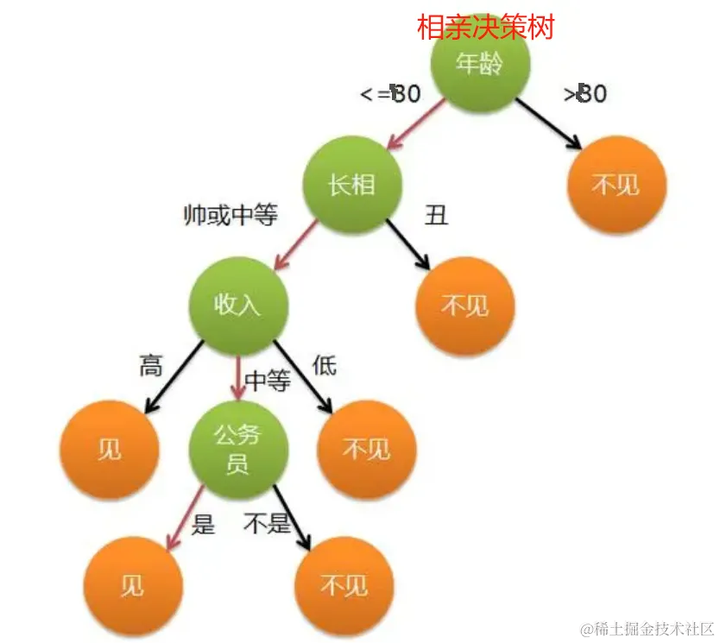
决策树回归是一种非参数模型,通过构建树状结构来进行预测。每个节点代表一个特征,分支代表该特征的取值,叶子节点代表预测结果。决策树回归通过递归地将数据集分割成更小的子集,直至满足停止条件。
原理:
决策树通过递归地将数据集分割成更小的子集来构建树状模型。每个内部节点代表一个特征,每个分支代表该特征的一个取值,每个叶节点代表一个类别或预测值。决策树的构建过程包括以下步骤:
选择最优特征:根据某种指标(如信息增益、基尼系数)选择最优特征进行分割。
分割数据集:根据选择的特征将数据集分割成子集。
递归构建子树:对子集递归调用上述步骤,直到满足停止条件(如所有数据点属于同一类别或达到最大深度)。
信息增益:信息增益用于衡量某一特征对数据集进行分割时所带来的信息熵的减少。信息熵(Entropy)表示数据集的纯度,计算公式为:
基尼系数:基尼系数(Gini Index)用于衡量数据集的不纯度,计算公式为:
适用场景和优点
决策树回归适用于处理非线性关系、缺失数据和特征交互复杂的情况。其主要优点包括:易于理解和解释、处理分类和回归任务、对数据预处理要求低。
实际案例和代码示例
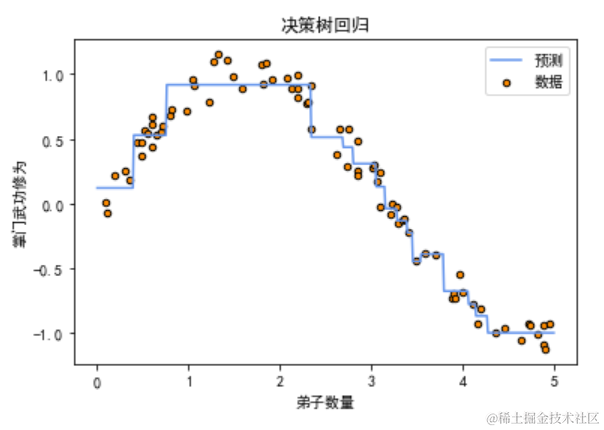
假设我们有一组数据,记录了某武侠小说中不同门派的弟子数量、门派成立时间、武器种类数量以及掌门的武功修为。我们可以使用决策树回归来预测这些因素对掌门武功修为的影响。
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.tree import DecisionTreeRegressor
# 生成示例数据np.random.seed(0)disciple_count = np.sort(5 * np.random.rand(80, 1), axis=0)master_skill = np.sin(disciple_count).ravel() + np.random.randn(80) * 0.1
# 使用决策树回归进行建模tree_model = DecisionTreeRegressor(max_depth=4)tree_model.fit(disciple_count, master_skill)
# 预测新数据点disciple_count_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]master_skill_pred = tree_model.predict(disciple_count_test)
# 绘制数据点和决策树回归曲线plt.scatter(disciple_count, master_skill, s=20, edgecolor="black", c="darkorange", label="数据")plt.plot(disciple_count_test, master_skill_pred, color="cornflowerblue", label="预测")plt.xlabel("弟子数量")plt.ylabel("掌门武功修为")plt.title("决策树回归")plt.legend()plt.show()
复制代码
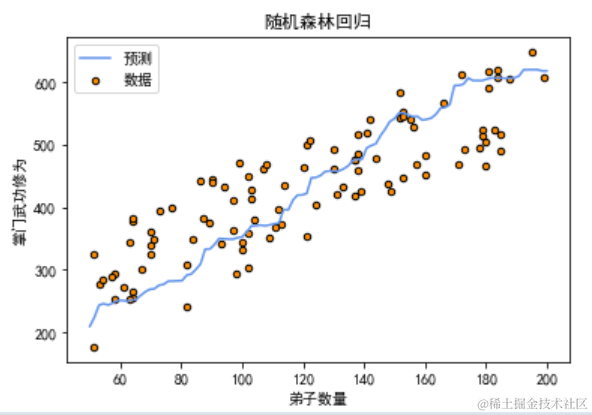
六、随机森林回归
定义和背景
随机森林回归是一种集成学习方法,通过构建多个决策树并对其结果进行平均,来提高模型的预测性能和稳定性。它通过引入随机性来构建多样化的决策树,从而减少过拟合和提高泛化能力。
适用场景和优点
随机森林回归适用于处理非线性关系、大规模数据集和特征间复杂交互的情况。其主要优点包括:高精度预测、对数据预处理要求低、处理缺失数据的能力强、可以评估特征重要性。
实际案例和代码示例
假设我们有一组数据,记录了某武侠小说中不同门派的弟子数量、门派成立时间、武器种类数量以及掌门的武功修为。我们可以使用随机森林回归来预测这些因素对掌门武功修为的影响。
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.ensemble import RandomForestRegressor
# 生成模拟数据np.random.seed(42)disciple_count = np.random.randint(50, 200, size=100)establishment_years = np.random.randint(1, 100, size=100)weapon_types = np.random.randint(1, 10, size=100)master_skill = 2 * disciple_count + 1.5 * establishment_years + 3 * weapon_types + np.random.randn(100) * 20 + 100
# 数据转换为二维数组X = np.column_stack((disciple_count, establishment_years, weapon_types))y = master_skill
# 创建随机森林回归模型并训练forest_reg = RandomForestRegressor(n_estimators=100, random_state=42)forest_reg.fit(X, y)
# 预测新数据点X_test = np.column_stack((np.linspace(50, 200, 100), np.linspace(1, 100, 100), np.linspace(1, 10, 100)))y_pred = forest_reg.predict(X_test)
# 可视化随机森林回归结果plt.scatter(disciple_count, master_skill, s=20, edgecolor="black", c="darkorange", label="数据")plt.plot(np.linspace(50, 200, 100), y_pred, color="cornflowerblue", label="预测")plt.xlabel("弟子数量")plt.ylabel("掌门武功修为")plt.title("随机森林回归")plt.legend()plt.show()
复制代码
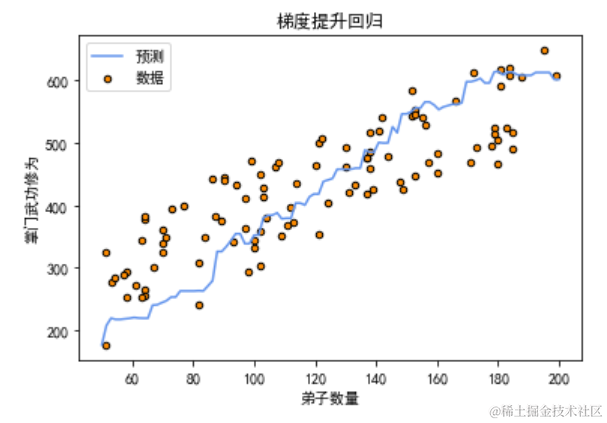
七、梯度提升回归
定义和背景
梯度提升回归(Gradient Boosting Regression)是一种集成学习方法,通过逐步构建多个弱学习器(通常是决策树),每个新的学习器都在之前学习器的基础上进行改进,以减少预测误差。其核心思想是通过逐步优化损失函数,最终得到一个强学习器。
适用场景和优点
梯度提升回归适用于处理非线性关系、复杂数据集和特征间的复杂交互。其主要优点包括:高精度预测、强大的处理非线性关系能力、较好的鲁棒性、能够处理缺失数据。
实际案例和代码示例
假设我们有一组数据,记录了某武侠小说中不同门派的弟子数量、门派成立时间、武器种类数量以及掌门的武功修为。我们可以使用梯度提升回归来预测这些因素对掌门武功修为的影响。
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.ensemble import GradientBoostingRegressor
# 生成模拟数据np.random.seed(42)disciple_count = np.random.randint(50, 200, size=100)establishment_years = np.random.randint(1, 100, size=100)weapon_types = np.random.randint(1, 10, size=100)master_skill = 2 * disciple_count + 1.5 * establishment_years + 3 * weapon_types + np.random.randn(100) * 20 + 100
# 数据转换为二维数组X = np.column_stack((disciple_count, establishment_years, weapon_types))y = master_skill
# 创建梯度提升回归模型并训练gbr_model = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1, max_depth=3, random_state=42)gbr_model.fit(X, y)
# 预测新数据点X_test = np.column_stack((np.linspace(50, 200, 100), np.linspace(1, 100, 100), np.linspace(1, 10, 100)))y_pred = gbr_model.predict(X_test)
# 可视化梯度提升回归结果plt.scatter(disciple_count, master_skill, s=20, edgecolor="black", c="darkorange", label="数据")plt.plot(np.linspace(50, 200, 100), y_pred, color="cornflowerblue", label="预测")plt.xlabel("弟子数量")plt.ylabel("掌门武功修为")plt.title("梯度提升回归")plt.legend()plt.show()
复制代码
八、支持向量回归
定义和背景
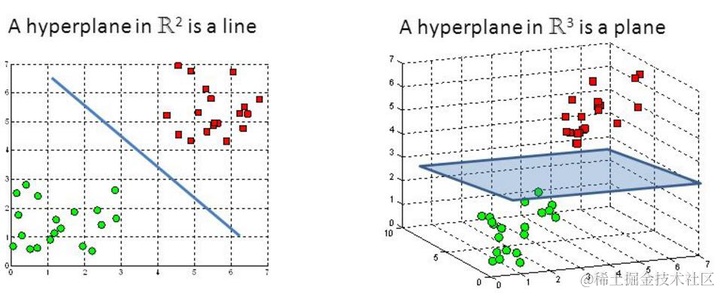
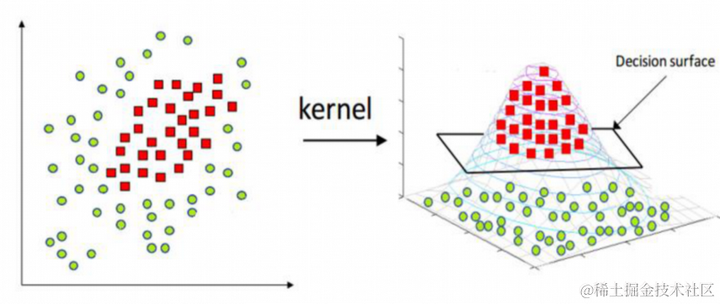
支持向量回归(Support Vector Regression,SVR)是支持向量机(Support Vector Machine,SVM)的一个变种,用于回归问题。SVR 通过在高维空间中寻找一个最佳的超平面,以最小化预测误差。其核心思想是通过核函数将低维特征映射到高维特征空间,从而处理非线性回归问题。
适用场景和优点
支持向量回归适用于处理高维数据、非线性关系和小样本数据集。其主要优点包括:高精度预测、处理非线性关系的能力、对噪声数据的鲁棒性、适用于高维特征空间。
实际案例和代码示例
假设我们有一组数据,记录了某武侠小说中不同门派的弟子数量、门派成立时间、武器种类数量以及掌门的武功修为。我们可以使用支持向量回归来预测这些因素对掌门武功修为的影响。
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.svm import SVR
# 生成模拟数据np.random.seed(42)disciple_count = np.sort(5 * np.random.rand(80, 1), axis=0)master_skill = np.sin(disciple_count).ravel() + np.random.randn(80) * 0.1
# 使用支持向量回归进行建模svr_model = SVR(kernel='rbf', C=100, gamma=0.1, epsilon=0.1)svr_model.fit(disciple_count, master_skill)
# 预测新数据点disciple_count_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]master_skill_pred = svr_model.predict(disciple_count_test)
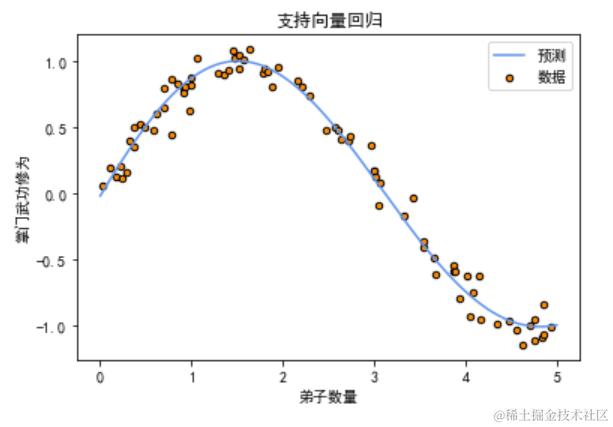
# 绘制数据点和支持向量回归曲线plt.scatter(disciple_count, master_skill, s=20, edgecolor="black", c="darkorange", label="数据")plt.plot(disciple_count_test, master_skill_pred, color="cornflowerblue", label="预测")plt.xlabel("弟子数量")plt.ylabel("掌门武功修为")plt.title("支持向量回归")plt.legend()plt.show()
复制代码
九、XGBoost 回归
定义和背景
XGBoost(Extreme Gradient Boosting)是一种增强型的梯度提升算法,因其高效、灵活和准确性高而在数据科学竞赛中广受欢迎。XGBoost 通过逐步构建多个决策树,优化损失函数来减少误差,并引入正则化项以防止过拟合。
适用场景和优点
XGBoost 回归适用于大规模数据集、非线性关系、特征间复杂交互以及高维数据。其主要优点包括:高预测精度、快速训练速度、处理缺失数据的能力、自动特征选择和正则化防止过拟合。
实际案例和代码示例
假设我们有一组数据,记录了某武侠小说中不同门派的弟子数量、门派成立时间、武器种类数量以及掌门的武功修为。我们可以使用 XGBoost 回归来预测这些因素对掌门武功修为的影响。
import numpy as npimport matplotlib.pyplot as pltimport xgboost as xgb
# 生成模拟数据np.random.seed(42)disciple_count = np.random.randint(50, 200, size=100)establishment_years = np.random.randint(1, 100, size=100)weapon_types = np.random.randint(1, 10, size=100)master_skill = 2 * disciple_count + 1.5 * establishment_years + 3 * weapon_types + np.random.randn(100) * 20 + 100
# 数据转换为二维数组X = np.column_stack((disciple_count, establishment_years, weapon_types))y = master_skill
# 创建DMatrix数据结构dtrain = xgb.DMatrix(X, label=y)
# 设置参数params = { 'objective': 'reg:squarederror', 'max_depth': 3, 'eta': 0.1, 'seed': 42}
# 训练XGBoost模型bst = xgb.train(params, dtrain, num_boost_round=100)
# 预测新数据点X_test = np.column_stack((np.linspace(50, 200, 100), np.linspace(1, 100, 100), np.linspace(1, 10, 100)))dtest = xgb.DMatrix(X_test)y_pred = bst.predict(dtest)
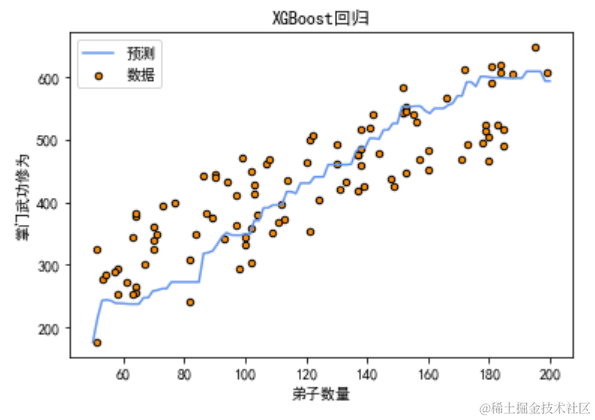
# 可视化XGBoost回归结果plt.scatter(disciple_count, master_skill, s=20, edgecolor="black", c="darkorange", label="数据")plt.plot(np.linspace(50, 200, 100), y_pred, color="cornflowerblue", label="预测")plt.xlabel("弟子数量")plt.ylabel("掌门武功修为")plt.title("XGBoost回归")plt.legend()plt.show()
复制代码
十、LightGBM 回归
定义和背景
LightGBM(Light Gradient Boosting Machine)是一种高效的梯度提升框架,由微软公司开发,主要用于大数据集和高维数据的处理。LightGBM 通过基于直方图的决策树学习算法,显著提高了训练速度和内存效率,同时保持较高的预测精度。
适用场景和优点
LightGBM 回归适用于大规模数据集、高维特征空间和实时预测场景。其主要优点包括:高效的训练速度、低内存消耗、处理大规模数据和高维数据的能力、支持并行和分布式训练。
实际案例和代码示例
假设我们有一组数据,记录了某武侠小说中不同门派的弟子数量、门派成立时间、武器种类数量以及掌门的武功修为。我们可以使用 LightGBM 回归来预测这些因素对掌门武功修为的影响。
import numpy as npimport matplotlib.pyplot as pltimport lightgbm as lgb
# 生成模拟数据np.random.seed(42)disciple_count = np.random.randint(50, 200, size=100)establishment_years = np.random.randint(1, 100, size=100)weapon_types = np.random.randint(1, 10, size=100)master_skill = 2 * disciple_count + 1.5 * establishment_years + 3 * weapon_types + np.random.randn(100) * 20 + 100
# 数据转换为二维数组X = np.column_stack((disciple_count, establishment_years, weapon_types))y = master_skill
# 创建LightGBM数据集train_data = lgb.Dataset(X, label=y)
# 设置参数params = { 'objective': 'regression', 'metric': 'l2', 'boosting': 'gbdt', 'num_leaves': 31, 'learning_rate': 0.05, 'feature_fraction': 0.9}
# 训练LightGBM模型gbm = lgb.train(params, train_data, num_boost_round=100)
# 预测新数据点X_test = np.column_stack((np.linspace(50, 200, 100), np.linspace(1, 100, 100), np.linspace(1, 10, 100)))y_pred = gbm.predict(X_test)
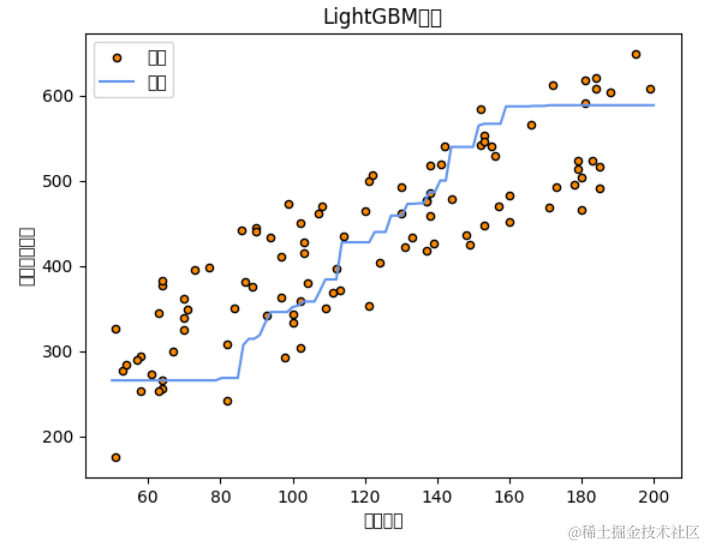
# 可视化LightGBM回归结果plt.scatter(disciple_count, master_skill, s=20, edgecolor="black", c="darkorange", label="数据")plt.plot(np.linspace(50, 200, 100), y_pred, color="cornflowerblue", label="预测")plt.xlabel("弟子数量")plt.ylabel("掌门武功修为")plt.title("LightGBM回归")plt.legend()plt.show()
复制代码
十一、神经网络回归
定义和背景
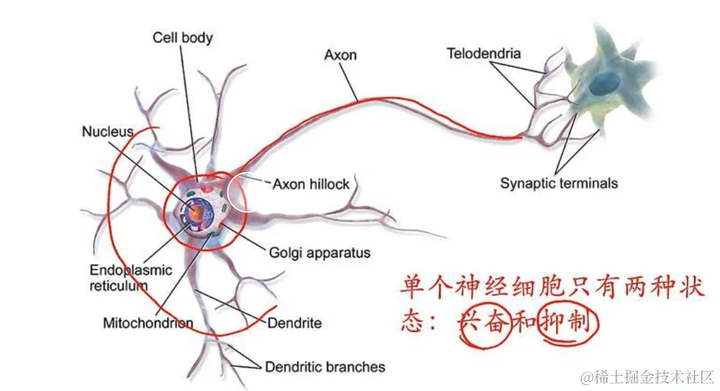
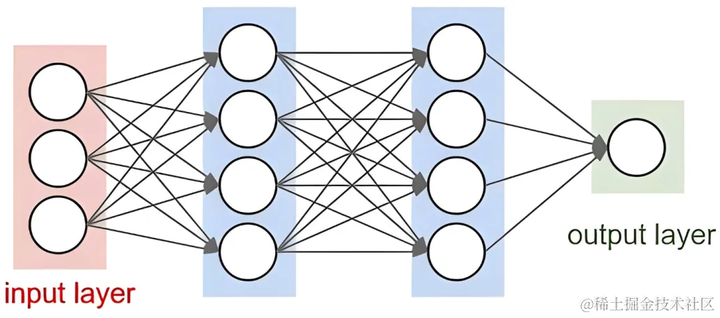
神经网络是一类受生物神经系统启发的机器学习算法,通过多个层次的神经元连接,能够捕捉复杂的非线性关系。神经网络回归利用多层感知机(MLP)等结构,通过反向传播算法调整权重,优化预测精度。
(gif by machinelearningknowledge.ai)
适用场景和优点
神经网络回归适用于处理非线性关系、复杂数据模式、大规模数据和高维数据。其主要优点包括:处理复杂非线性关系的能力、自动特征提取、高预测精度和广泛的应用范围。
实际案例和代码示例
假设我们有一组数据,记录了某武侠小说中不同门派的弟子数量、门派成立时间、武器种类数量以及掌门的武功修为。我们可以使用神经网络回归来预测这些因素对掌门武功修为的影响。
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.neural_network import MLPRegressor
# 生成模拟数据np.random.seed(42)disciple_count = np.random.randint(50, 200, size=100)establishment_years = np.random.randint(1, 100, size=100)weapon_types = np.random.randint(1, 10, size=100)master_skill = 2 * disciple_count + 1.5 * establishment_years + 3 * weapon_types + np.random.randn(100) * 20 + 100
# 数据转换为二维数组X = np.column_stack((disciple_count, establishment_years, weapon_types))y = master_skill
# 使用神经网络回归进行建模nn_model = MLPRegressor(hidden_layer_sizes=(50, 50), max_iter=1000, random_state=42)nn_model.fit(X, y)
# 预测新数据点X_test = np.column_stack((np.linspace(50, 200, 100), np.linspace(1, 100, 100), np.linspace(1, 10, 100)))y_pred = nn_model.predict(X_test)
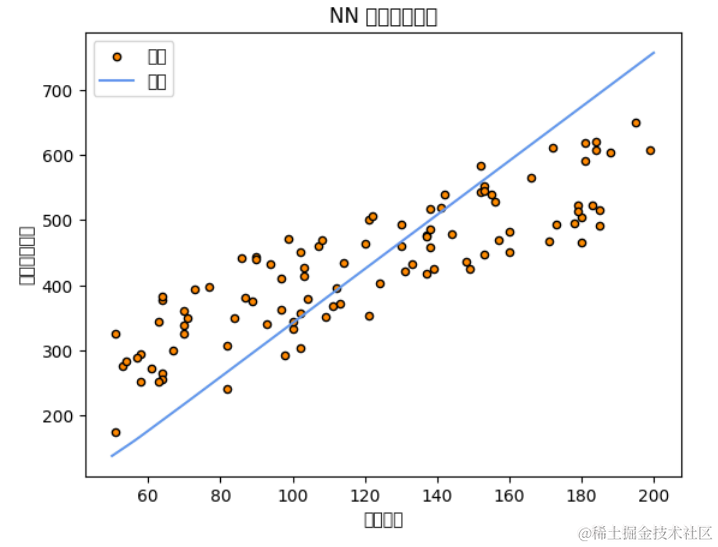
# 可视化神经网络回归结果plt.scatter(disciple_count, master_skill, s=20, edgecolor="black", c="darkorange", label="数据")plt.plot(np.linspace(50, 200, 100), y_pred, color="cornflowerblue", label="预测")plt.xlabel("弟子数量")plt.ylabel("掌门武功修为")plt.title("神经网络回归")plt.legend()plt.show()
复制代码
十二、逻辑回归
Emmm,逻辑回归不是回归算法,是分类算法。
逻辑回归是来打酱油的
文章转载自:算法金「全网同名」
原文链接:https://www.cnblogs.com/suanfajin/p/18221375
体验地址:http://www.jnpfsoft.com/?from=infoq
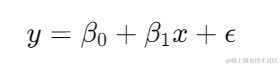
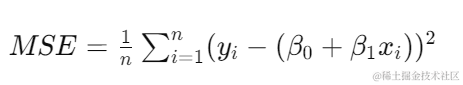
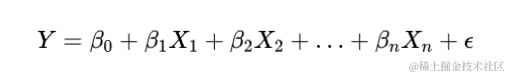

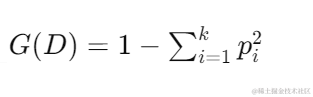








评论