暴力递归概念
暴力递归就是尝试
暴力递归手法技巧
1、把问题转化为规模更小的同类问题
2、有明确的不需要继续进行递归的条件(base case)
3、有当得到了子问题结果之后的决策过程
4、大问题调用小问题,那么大问题所做的决定对小问题产生的影响一定要在参数上体现出来,否则递归是写不出来的
具体问题
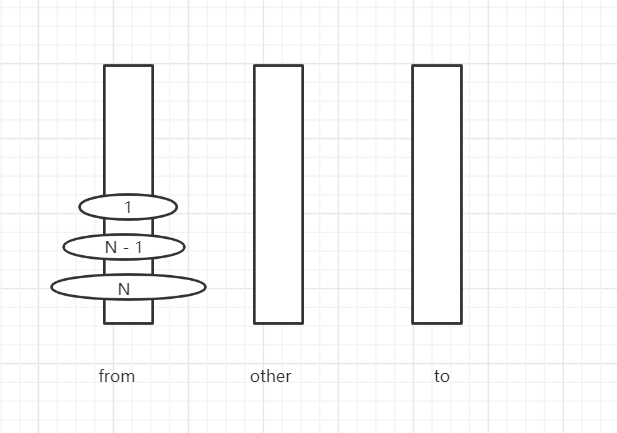
(一)汉诺塔问题
问题描述,就是有三个塔,要把 from 上面的盘子移到 to 上面去,注意这个盘是大小的,移动的时候无论怎么样只能小盘压在大盘上面,每次只能移动一个盘子
现在给你一个盘子的数量,然你打印出 移动的过程
思路分析 要从 from 移动到 to 那么 首先最大的那个盘子移动到 to 的时候,to 必然是空,否则就大盘压小盘了,那 from 要移动的话,那必要要情况 1...N-1 的盘,这些盘只能放在 other 中,OK,那么其实我们就可以写出这个递归了
public static void hanoi(int n) { if (n > 0) { func(n, "左", "中", "右"); }}
public static void func(int N, String from, String other, String to) { if (N <= 0) { return; } func(N - 1, from, to, other); System.out.println("Move " + N + " from " + from + " to " + to); func(N - 1, other, from, to);}
复制代码
套到上面的技巧, 首先是 base case 对吧
然后掉完子问题之后有个打印 这个就是决策过程
但是他的尝试模型呢?其实它并没有尝试模型,就是一个大问题调用子问题
(二)字符串的全部子序列
比如给你一个字符串 "abc" 那么你给我返回的子序列是['','a','b','c','ab','ac','bc','abc'] 就是空字符串也要
思路分析 abc 给我,那其实我就是从 a 开始然后做两个选择,这个 a 要或者不要,然后 b 要不要,c 要不要就行了,这是一个标准的从左到右的尝试模型
public static List<String> getAllSubs(String str) { char[] chars = str.toCharArray(); List<String> ans = new ArrayList<>(); process(chars, 0, ans, ""); return ans; }
/** * str[0..index-1] 的沿途决定,是path记录的 * str[index] 这个字符,都可以选择要还是不要 * @param str 传进来的str * @param index 当前的索引 * @param ans 递归传递的list * @param path 路劲 */ public static void process(char[] str, int index, List<String> ans, String path) { if (index == str.length) { ans.add(path); return; }
// 不要这个字符 process(str, index + 1, ans, path);
// 要这个字符 process(str, index + 1, ans, path + str[index]); }
复制代码
我们来看下怎么写的这个递归过程,首先 base case 就是 index 索引已经到了处理完 str 的长度了,那么就收集好这个 path,这个 path 就是沿途路劲所做的决定,在大问题调用子问题的过程中,所做的决定肯定会影响之后的结果,所以在参数上体现出来了
(三)背包问题
给定两个长度都为 N 的数组 weights 和 values, weights[i]和 values[i]分别代表 i 号物品的重量和价值。 给定一个正数 bag, 表示一个载重 bag 的袋子, 你装的物品不能超过这个重量。 返回你能装下最多的价值是多少?
其实也是一个标准的从左到右尝试模型,第一个要不要,第二个要不要,然后最后子问题调用完了 决策过程 就是判断哪种情况的收益大
public static int getMaxValue(int[] w, int[] v, int bag) { return process(w, v, 0, 0, bag); }
/** * 背包问题 暴力递归 * * @param w 物品 * @param v 价值 * @param index 前面已经决定过得索引 * @param alreadyW 背包已经使用的容量 * @param bag 背包的总容量 * @return 能装下的最大价值 */ private static int process(int[] w, int[] v, int index, int alreadyW, int bag) { if (alreadyW > bag) { return -1; }
if (index == w.length) { return 0; }
// 不要 int p1 = process(w, v, index + 1, alreadyW, bag);
// 要 int p2next = process(w, v, index + 1, alreadyW + w[index], bag);
int p2 = -1; if (p2next != -1) { p2 = v[index] + p2next; } return Math.max(p1, p2); }
复制代码






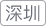






评论