算法攻关 - 二叉树最大深度 (O(n))_0104

小诚信驿站

关注

发布于: 2021 年 03 月 08 日

一、题目描述

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-depth-of-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

二、思考

首先我们要明确树的深度实际上就是我们遍历的时候树的高度，那么同样我们能想到的广度优先遍历 BFS，一层一层遍历，遍历多少层就是多高的树。或者深度优先遍历 DFS，找到遍历的最大长度即为树的高度。

三、代码实现

 class TreeNode{        private int val;        private TreeNode left;        private TreeNode right;        public TreeNode(int x){            this.val = x;        }        public TreeNode(int x,TreeNode left,TreeNode right){            this.val=x;            this.left=left;            this.right= right;        }    }
    public int maxDepth(TreeNode root) {        //第一步：处理特殊情况        if(root == null){            return 0;        }        //第二步、遍历左子树        int leftTree = maxDepth(root.left);        //第三步、遍历右子树        int rightTree = maxDepth(root.right);        //第四步、比较左右子树的高度，+1        return Math.max(leftTree,rightTree)+1;    }

复制代码

复杂度分析

时间复杂度：O(n)，其中 nn 为二叉树节点的个数。每个节点在递归中只被遍历一次。

空间复杂度：O(height)，其中 height 表示二叉树的高度。递归函数需要栈空间，而栈空间取决于递归的深度，因此空间复杂度等价于二叉树的高度。

如果是广度优先应该如何实现呢？

public int maxDepth2(TreeNode root) {        //第一步：处理特殊情况        if(root == null){            return 0;        }        //第二步：依赖外部数据结构队列，FIFO        Queue<TreeNode> queue = new LinkedList<>();        queue.offer(root);        int height=0;        //第三步：遍历队列        while(!queue.isEmpty()){            //第四步：明确每层叶子节点都可以遍历完毕            int size = queue.size();            while(size >0 ){                TreeNode node = queue.poll();                //遍历左叶子节点                if(node.left != null){                    queue.offer(node.left);                }                //遍历右叶子节点                if (node.right != null){                    queue.offer(node.right);                }                size--;            }            height++;        }        return height;    }

复制代码

复杂度分析

时间复杂度：O(n)，其中 nn 为二叉树的节点个数。与方法一同样的分析，每个节点只会被访问一次。

空间复杂度：此方法空间的消耗取决于队列存储的元素数量，其在最坏情况下会达到 O(n)。

四、小结

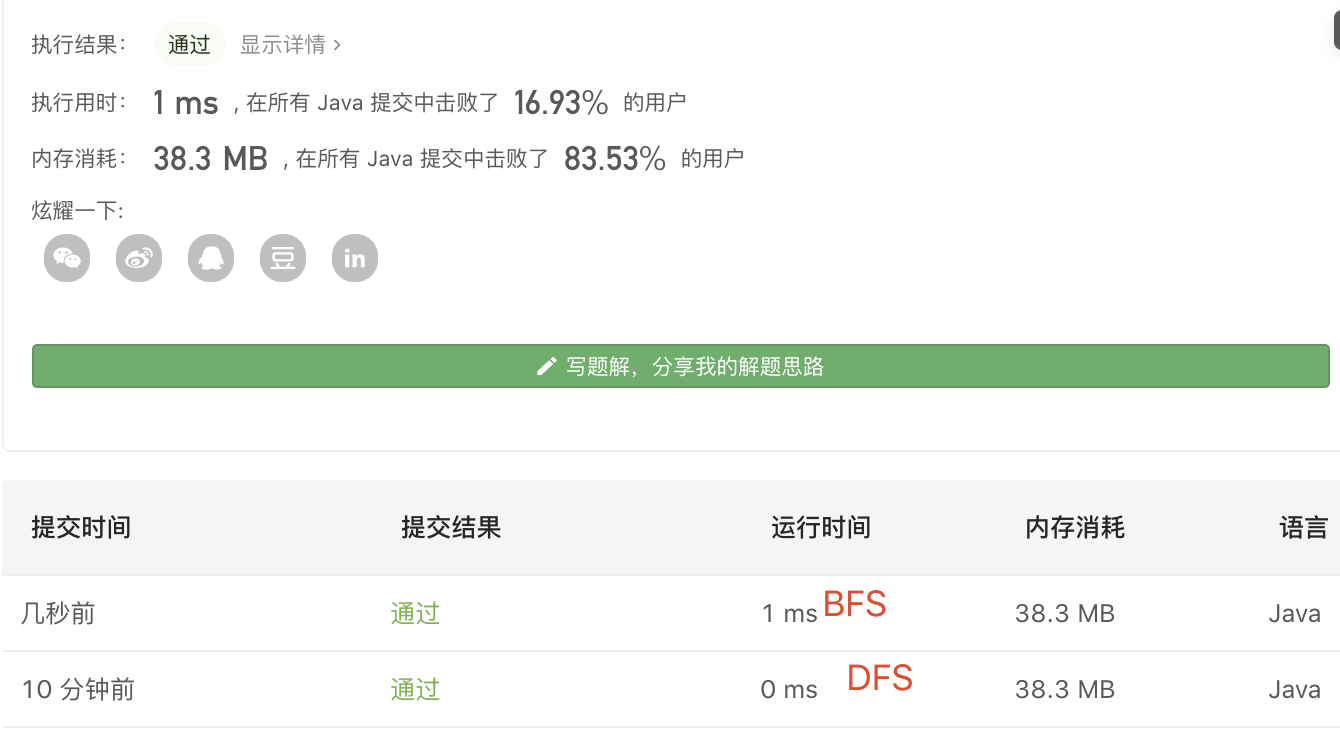
从结果来看还是 DFS 更好一些。

发布于: 2021 年 03 月 08 日阅读数: 16

原文链接:【http://xie.infoq.cn/article/93d86d44ba443b66c67ffcb85】。文章转载请联系作者。

小诚信驿站

关注

小胜靠智，大胜靠德 2019.06.27 加入

历经创业、京东、腾讯、滴滴公司，希望能够有些东西一起分享。公众号：小诚信驿站，微信/CSDN搜索：wolf_love666

发布

暂无评论

创作场景

算法攻关 - 二叉树最大深度 (O(n))_0104

一、题目描述

二、思考

三、代码实现

四、小结

小诚信驿站

评论