一、题目描述
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1输出:3解释:节点 5 和节点 1 的最近公共祖先是节点 3 。示例 2:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4输出:5解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。示例 3:
输入:root = [1,2], p = 1, q = 2输出:1
提示:
树中节点数目在范围 [2, 105] 内。-109 <= Node.val <= 109所有 Node.val 互不相同 。p != qp 和 q 均存在于给定的二叉树中。
来源:力扣(LeetCode)链接:https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
复制代码
二、思路
最近刷题的时候,突然发现是一种比较轻松的学习方式,吸取优秀的经验。所以如果遇到好的思路,我会直接使用好的思路方案,就不是自己的了。
以下思路出自大神的思路,我们来学习下:
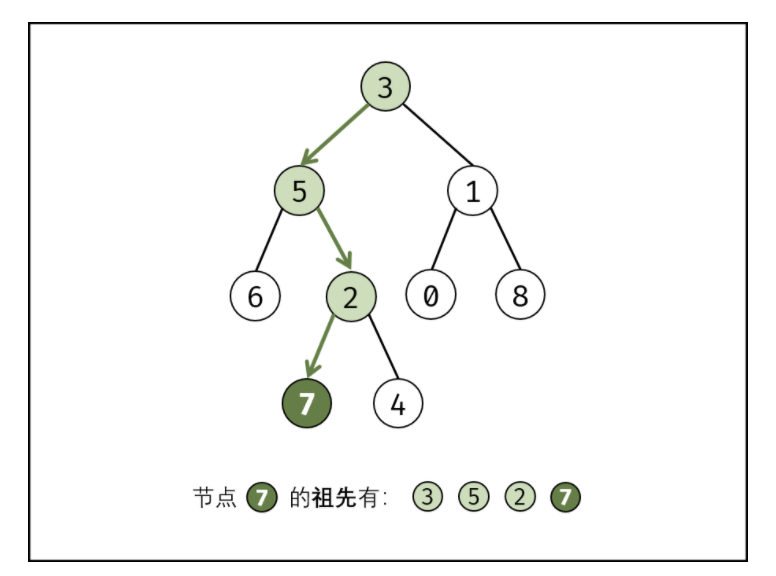
祖先的定义: 若节点 p 在节点 root 的左(右)子树中,或 p=root ,则称 root 是 p 的祖先。
在刷题之前我们数据结构入门中提到我们明确一种数据结构叫做二叉树:
二叉树
二叉树是树的一种特殊形式,二叉的意思是这种树的每个节点最多有 2 个孩子节点。(可以是没有,也可以是 1 个孩子节点)
我们现在再来看一张图
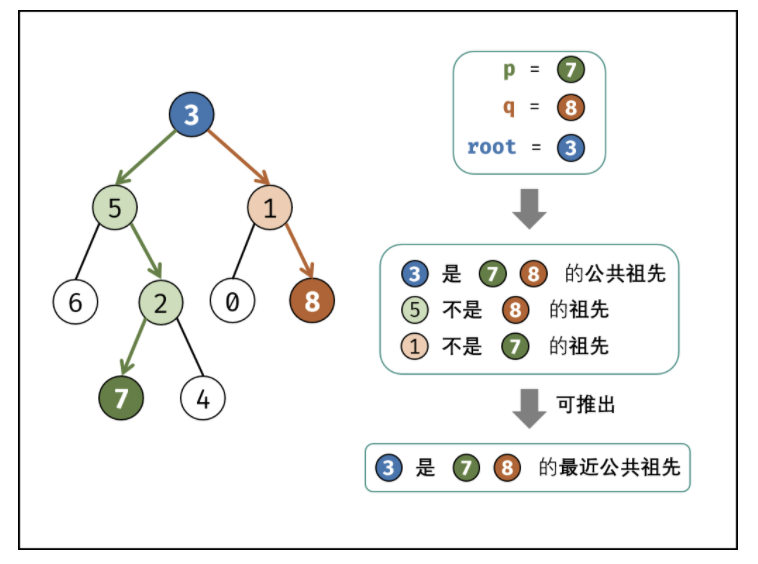
最近公共祖先的定义: 设节点 root 为节点 p, q 的某公共祖先,若其左子节点 root.left 和右子节点 root.right 都不是 p,q 的公共祖先,则称 root 是 “最近的公共祖先” 。
根据以上定义,若 root 是 p, q 的 最近公共祖先 ,则只可能为以下情况之一:
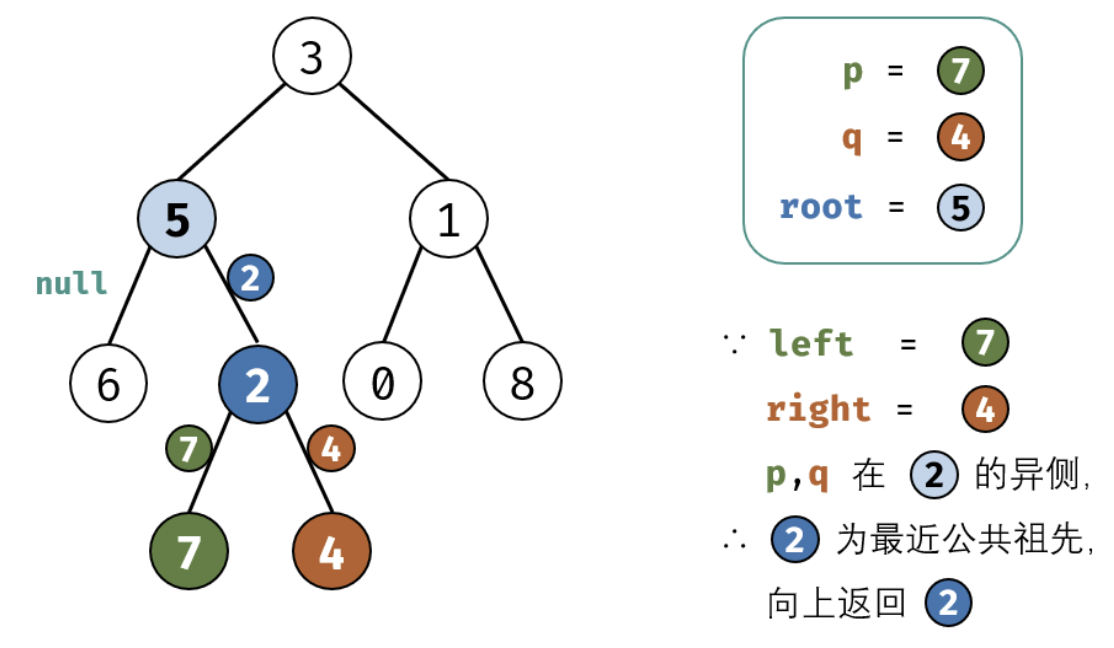
p 和 q 在 root 的子树中,且分列 root 的 异侧(即分别在左、右子树中);
p = root,且 q 在 root 的左或右子树中;
q = root ,且 p 在 root 的左或右子树中;
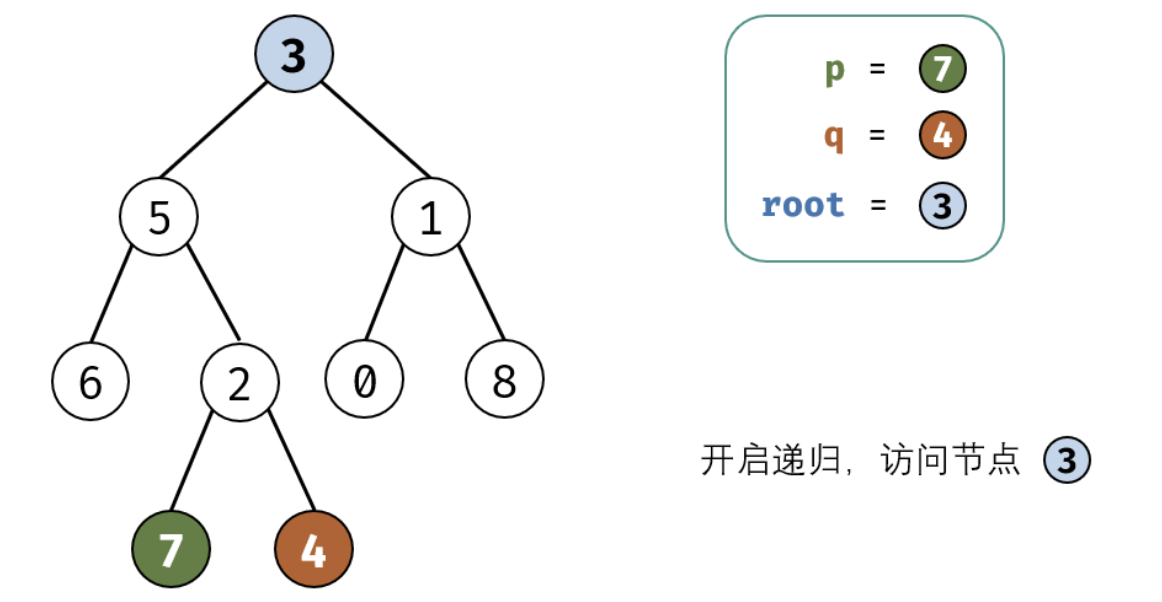
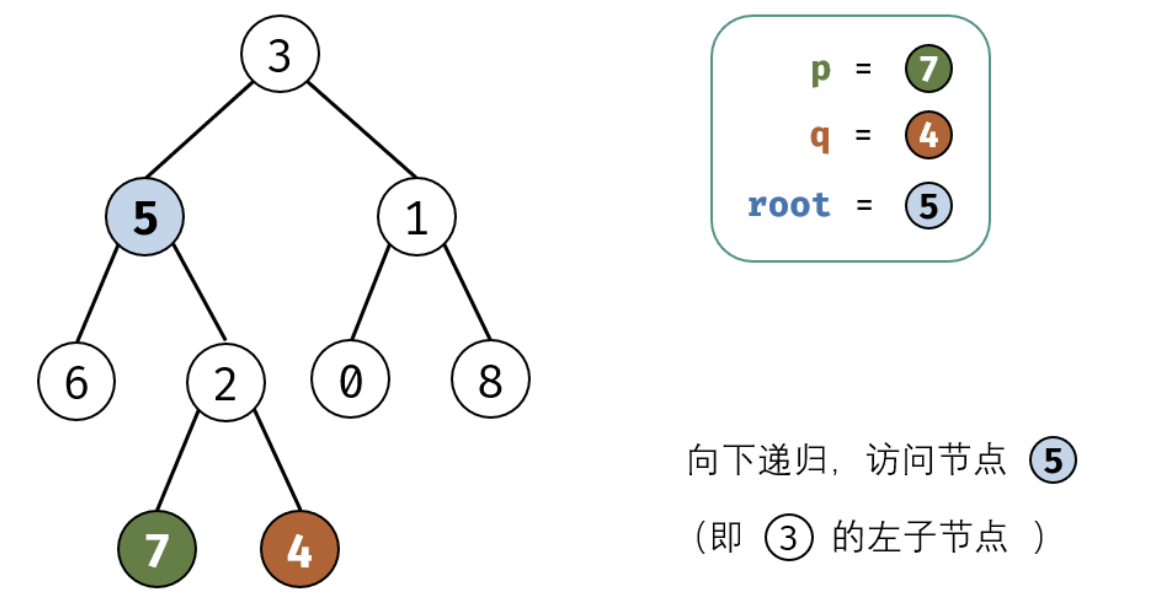
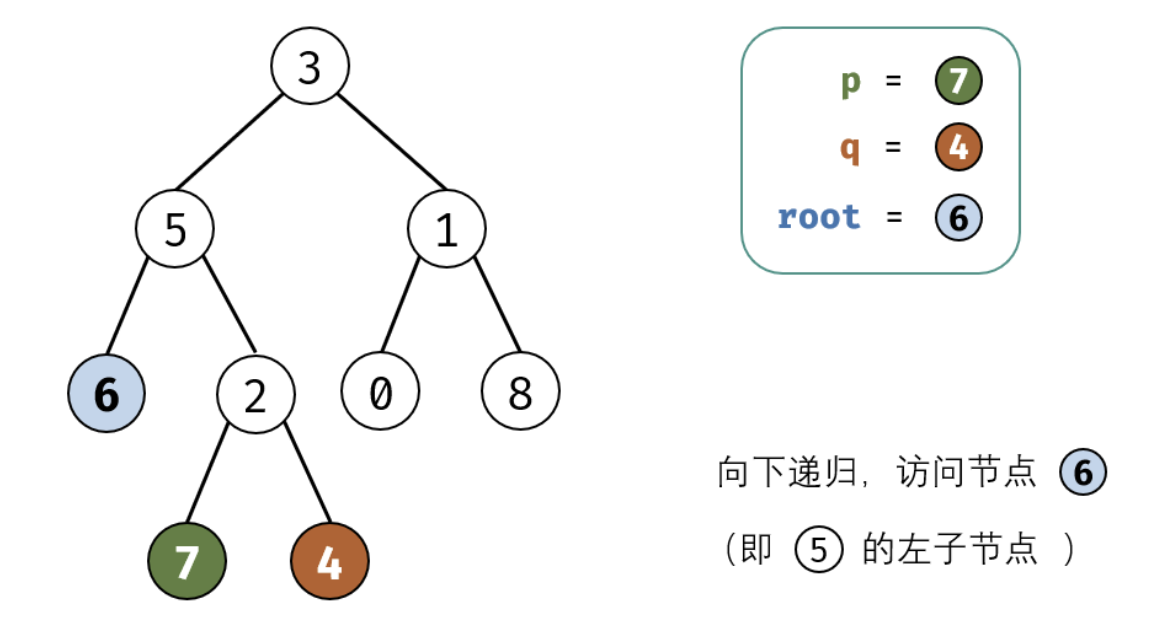
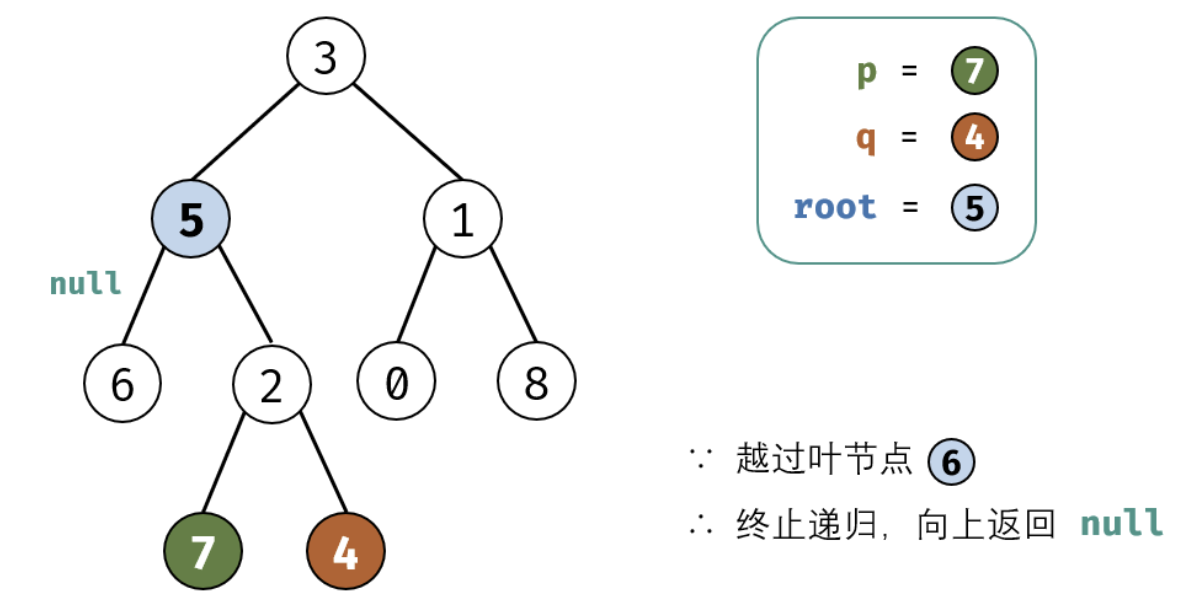
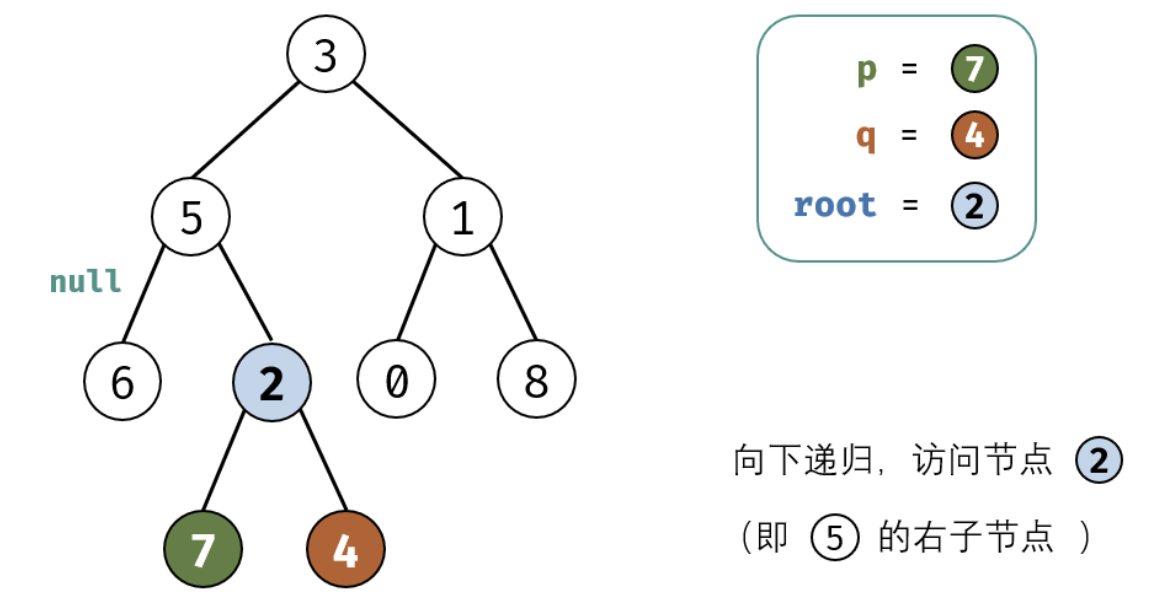
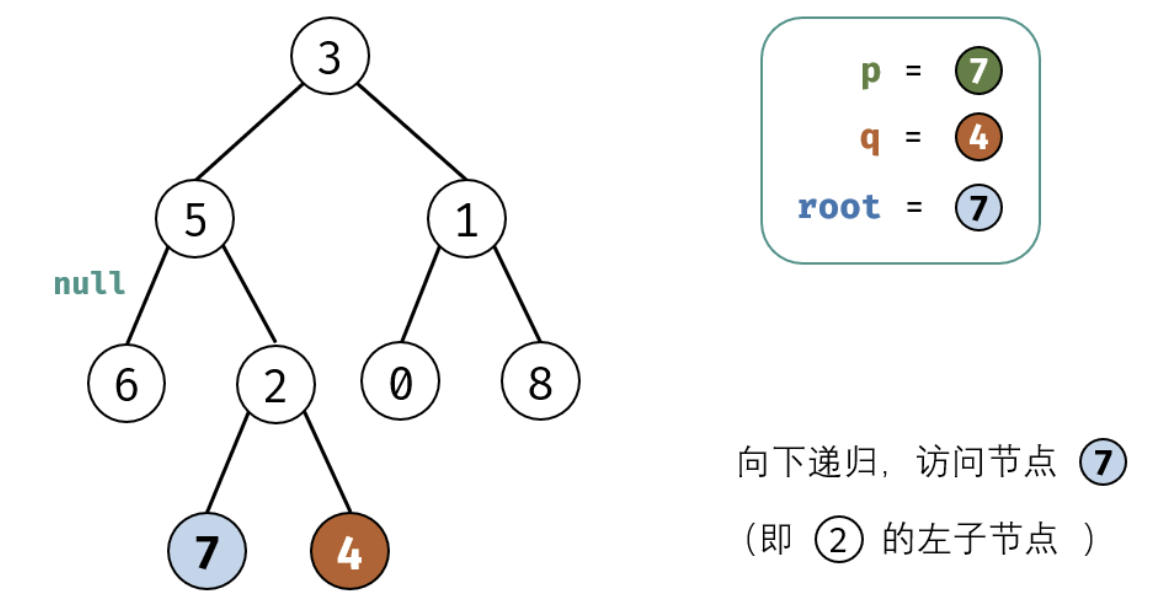
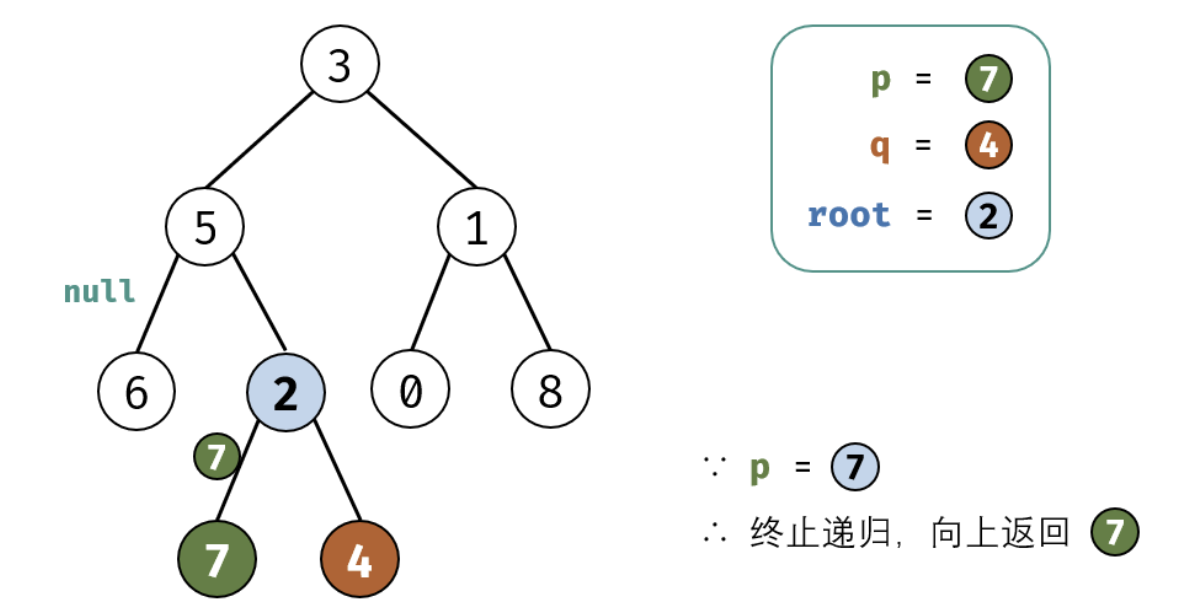
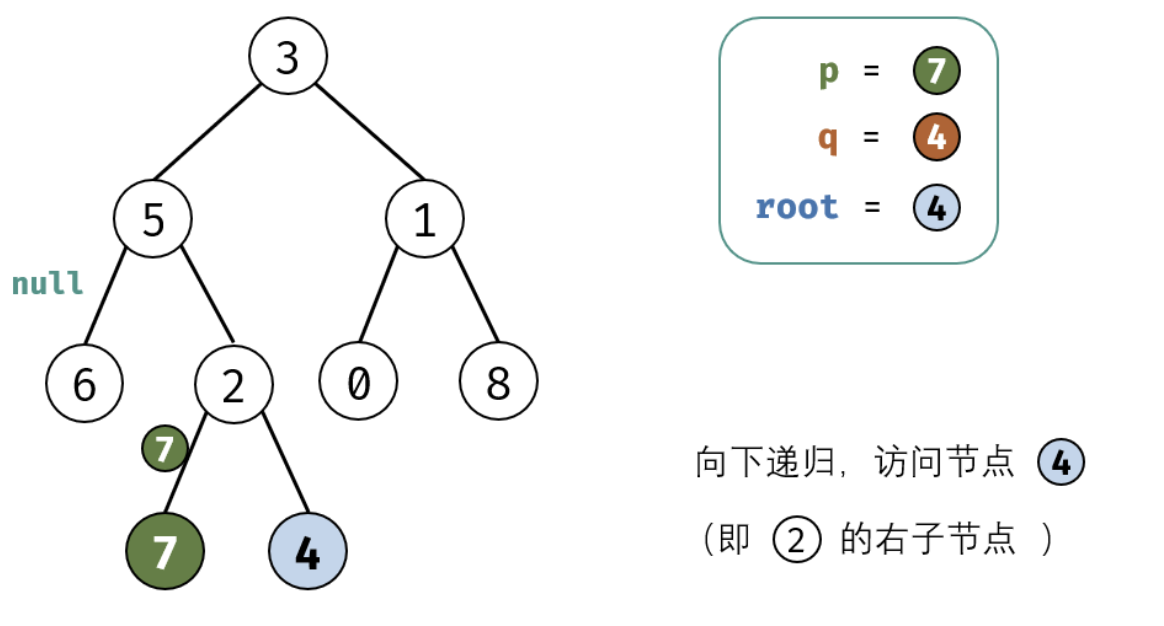
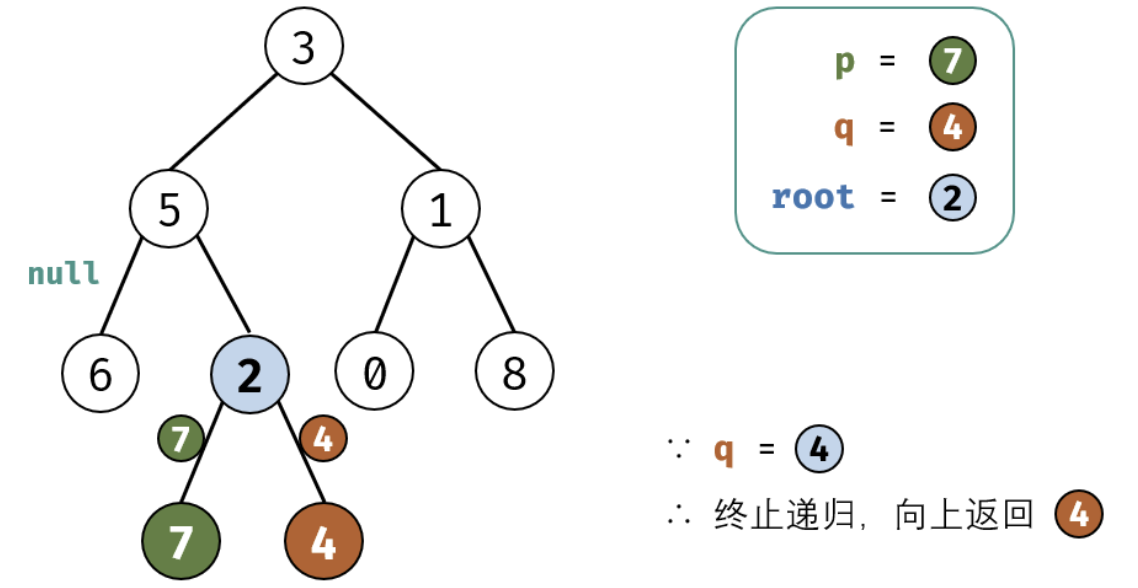
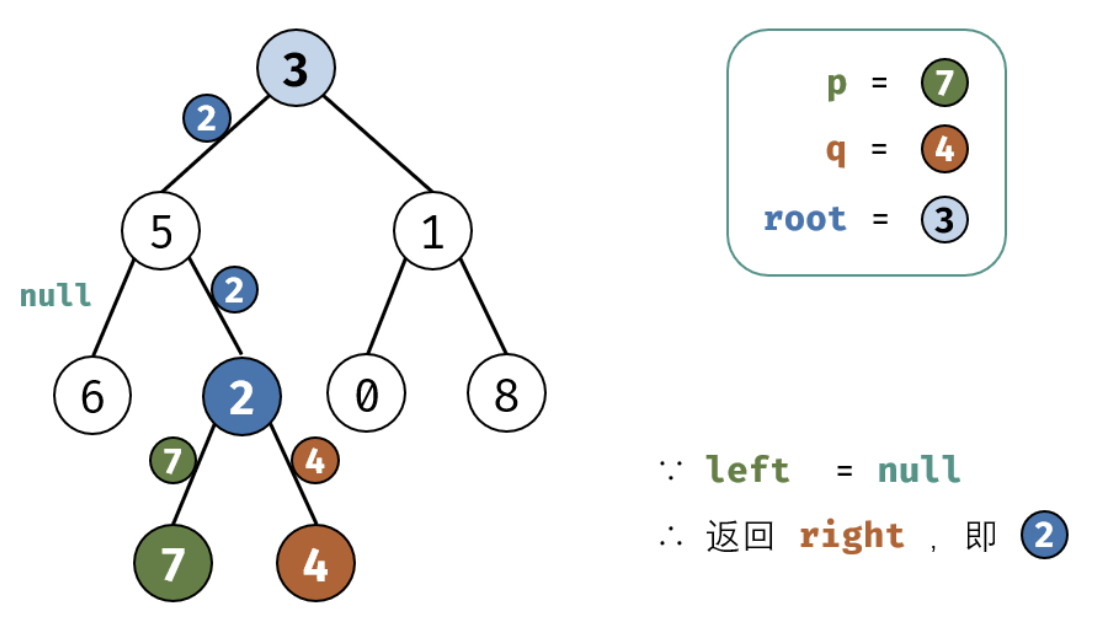
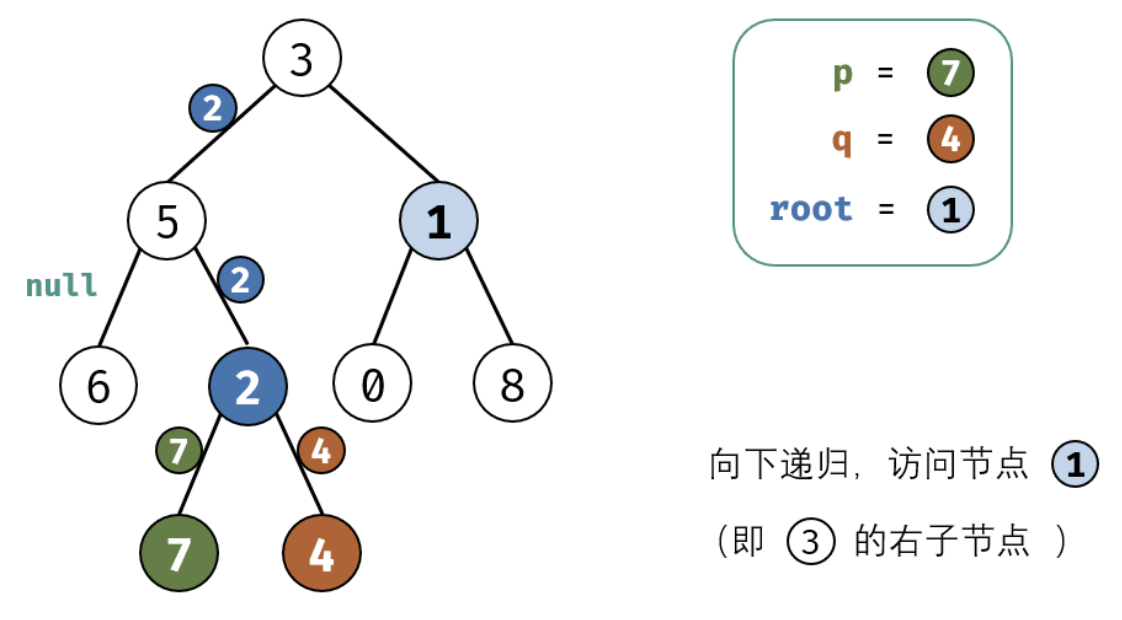
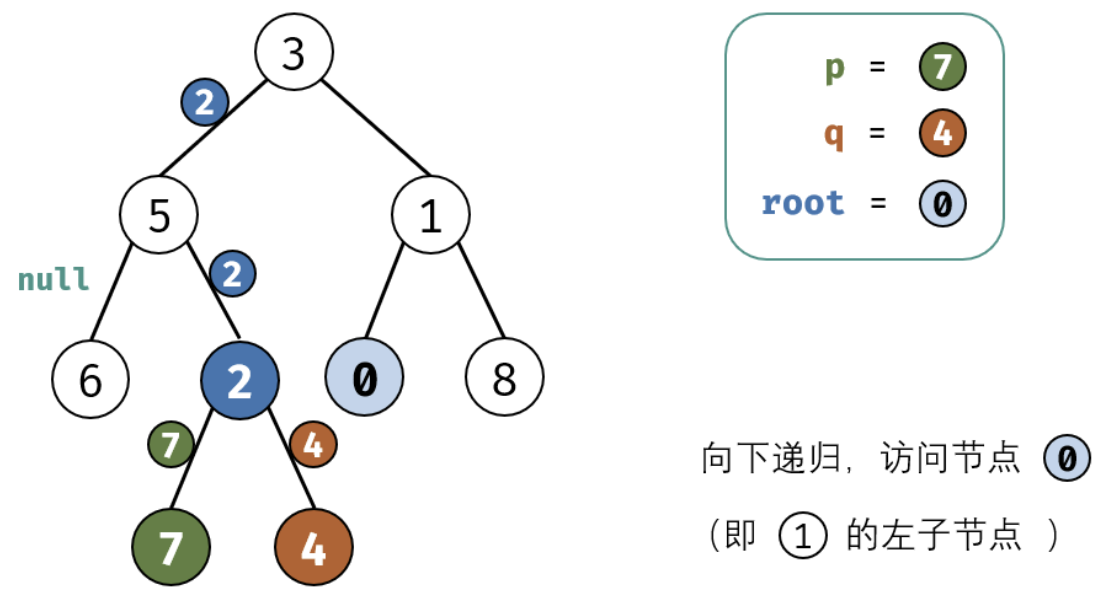
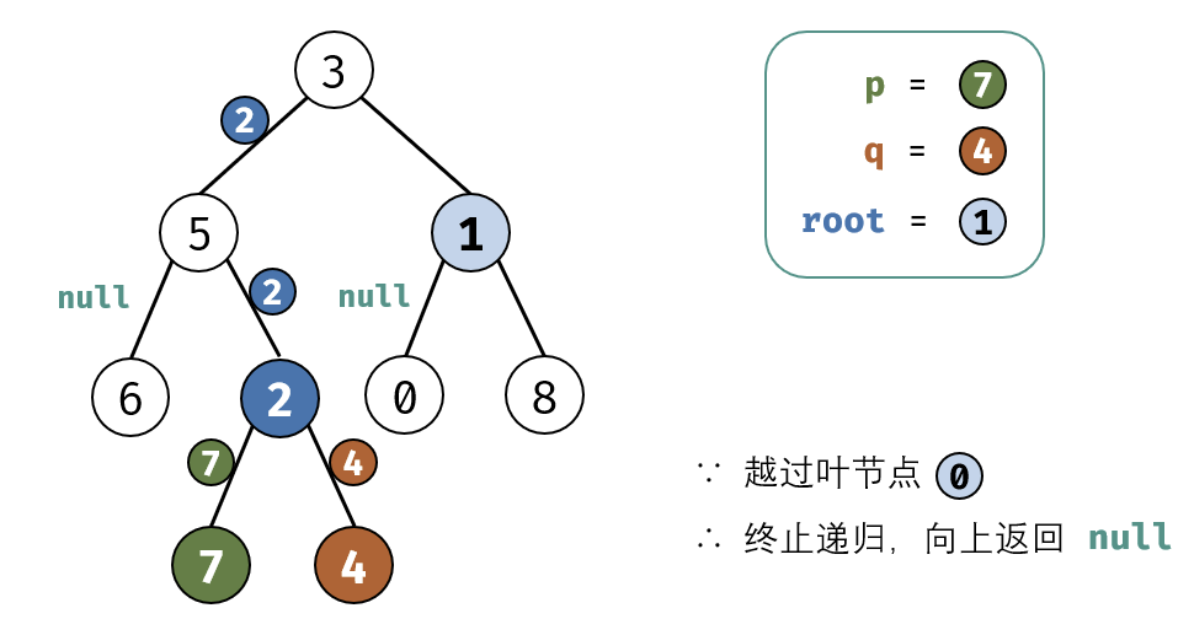
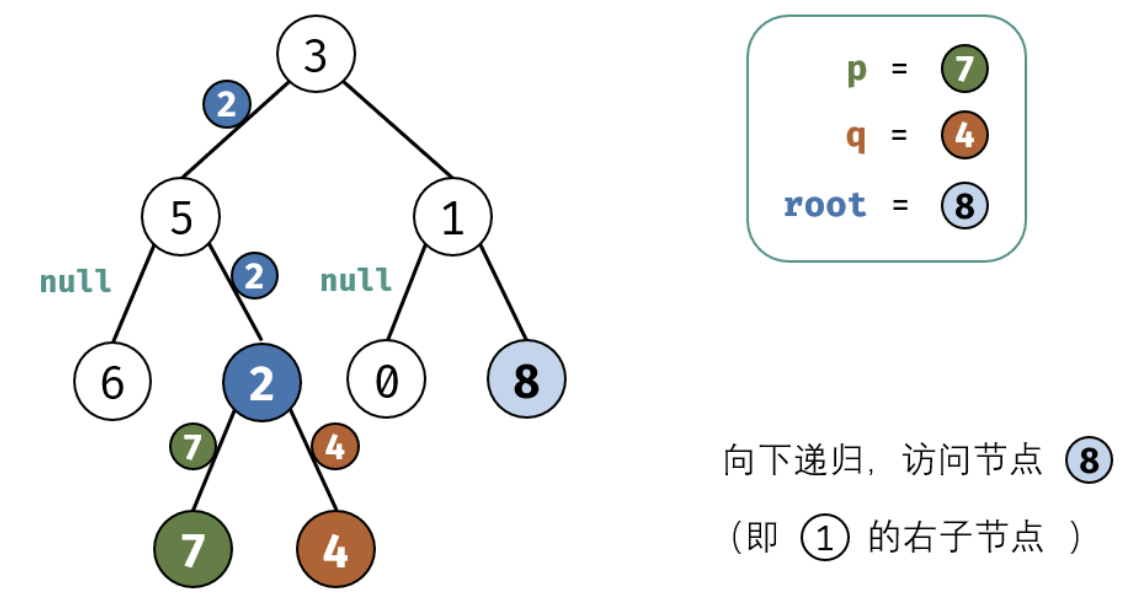
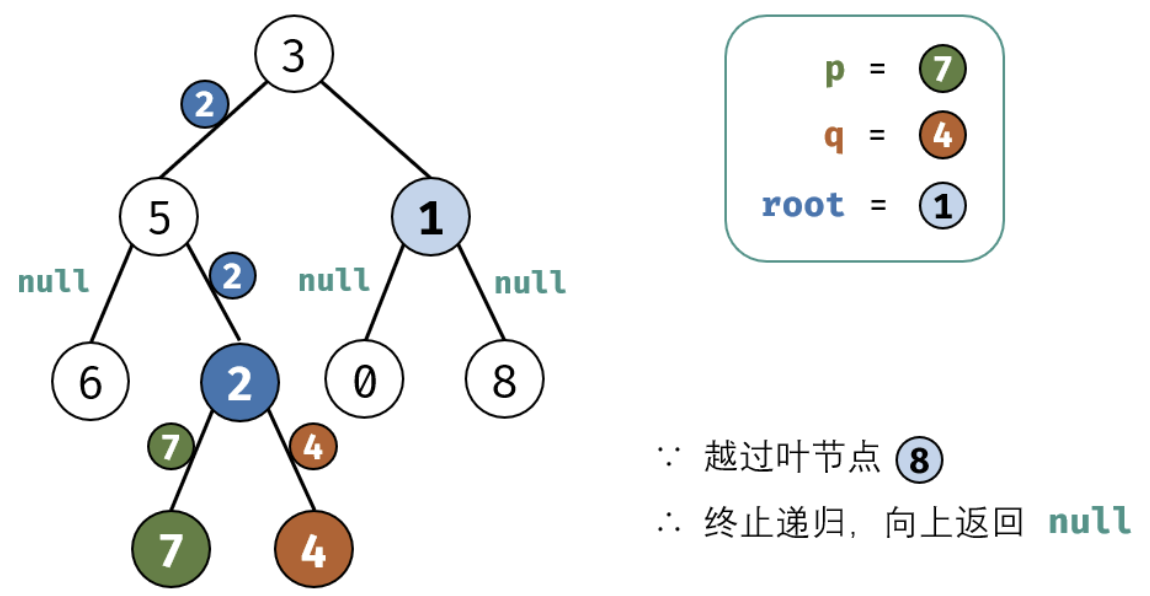
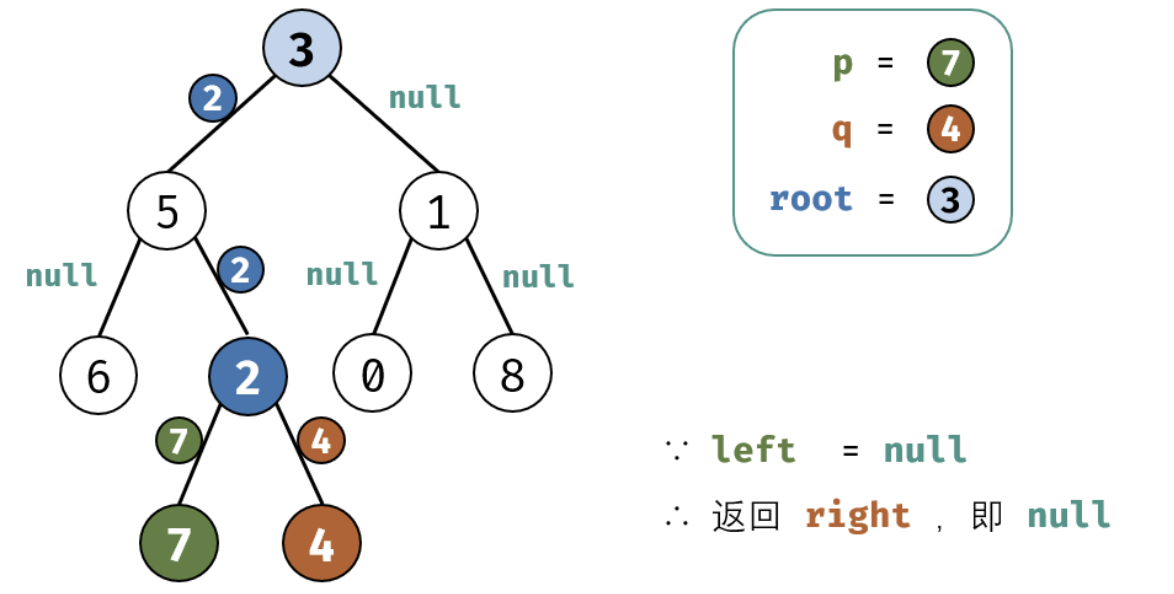
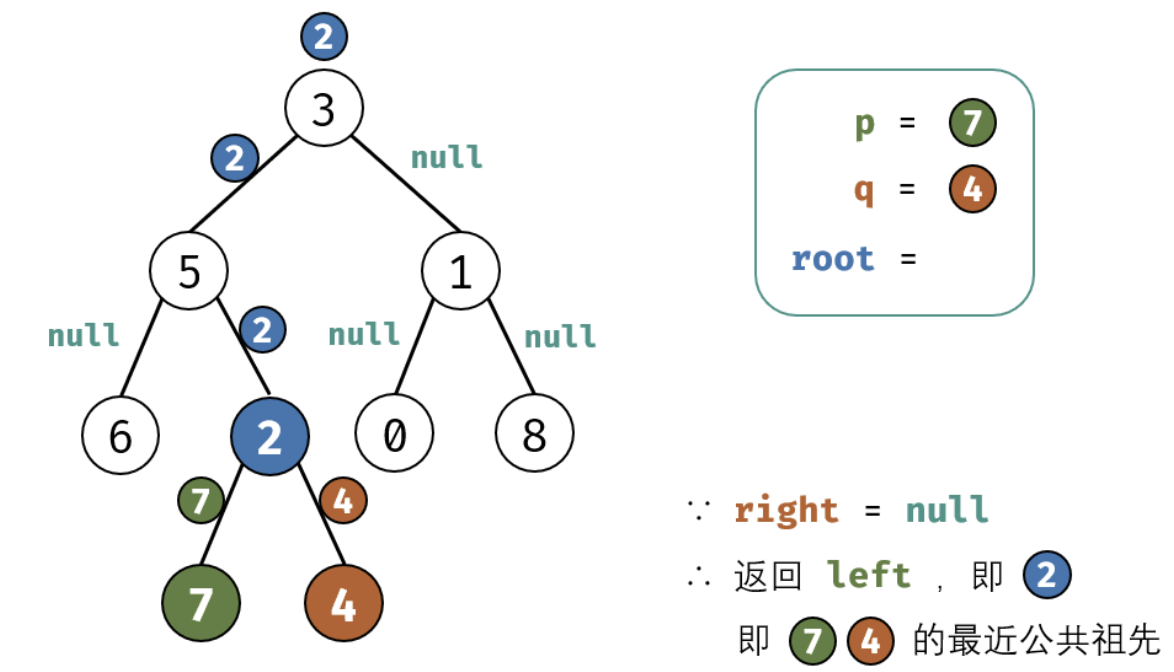
考虑通过递归对二叉树进行后序遍历,当遇到节点 p 或 q 时返回。从底至顶回溯,当节点 p,q 在节点 root 的异侧时,节点 root 即为最近公共祖先,则向上返回 root 。
这里面非常值的学习就是我们处理递归的时候需要首先要提取出终止条件,并需要递归的内容,以及每次递归返回值的确认。下面是图画讲解
复杂度分析:
时间复杂度 O(N) : 其中 N 为二叉树节点数;最差情况下,需要递归遍历树的所有节点。
空间复杂度 O(N): 最差情况下,递归深度达到 N ,系统使用 O(N) 大小的额外空间。
三、代码实现
/** * 定义一个二叉树,二叉树具有左右子树 */ public class TreeNode { int val; TreeNode left; TreeNode right; TreeNode(int x) { val = x; } }
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { //第一步、我们需要处理的是递归过程中的终止条件,一共分为三类,root=null、root=p、root=q if(root == null || root ==p || root == q){ return root; } //第二步、如果root节点不是公共父节点,则我们需要按照左子树、右子树去查找 TreeNode left = lowestCommonAncestor(root.left,p,q); TreeNode right = lowestCommonAncestor(root.right,p,q); //第三步、我们需要判断下如果left左子树为null,我们直接返回右子树,如果right右子树为null的话,返回左子树 //第四步、如果说左右子树都不为null,则我们认为root即为最小公共父节点 return left == null ? right : right == null ? left : root; }
复制代码
四、小结
这里面还有其他解法,比如我觉得好的一种思路是我们利用深度优先搜索,第一步先找到 P 的父亲节点,依次从底向上将子节点对应的父节点一一维护到字典表 map 中,然后我们继续深度优先搜索,找到 Q 的父亲节点等同于 P 的父亲节点则为最小公共父节点。如果没有找到,则返回 null。
代码也很好理解,如下
class Solution { Map<Integer, TreeNode> parent = new HashMap<Integer, TreeNode>(); Set<Integer> visited = new HashSet<Integer>();
public void dfs(TreeNode root) { if (root.left != null) { parent.put(root.left.val, root); dfs(root.left); } if (root.right != null) { parent.put(root.right.val, root); dfs(root.right); } }
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { dfs(root); while (p != null) { visited.add(p.val); p = parent.get(p.val); } while (q != null) { if (visited.contains(q.val)) { return q; } q = parent.get(q.val); } return null; }}
复制代码
复杂度分析
时间复杂度:O(N)O(N),其中 NN 是二叉树的节点数。二叉树的所有节点有且只会被访问一次,从 p 和 q 节点往上跳经过的祖先节点个数不会超过 NN,因此总的时间复杂度为 O(N)O(N)。
空间复杂度:O(N)O(N) ,其中 NN 是二叉树的节点数。递归调用的栈深度取决于二叉树的高度,二叉树最坏情况下为一条链,此时高度为 NN,因此空间复杂度为 O(N)O(N),哈希表存储每个节点的父节点也需要 O(N)O(N) 的空间复杂度,因此最后总的空间复杂度为 O(N)O(N)。
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/er-cha-shu-de-zui-jin-gong-gong-zu-xian-lcof/solution/er-cha-shu-de-zui-jin-gong-gong-zu-xian-6fdt7/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。













评论